Examining Schools

One of the major markers of education in America - and one that is often noted by observers abroad - is the degree of constant self-examination. In the U.S. today, when pupils and students are tested, so, in effect, are their teachers, the curricula, the schools and universities, and the entire set of systems.

Each year hundreds of research studies are published which critically examine the nation's schools. Most of the large school districts employ full-time educational researchers. Almost all of the universities have departments for educational research and measurement. And, of course, there are many public and private institutes, educational commissions, think tanks, foundations, and professional organisations, which publish their reports and studies and voice their opinions. Newspapers publicly report the test results of local schools each year. These are compared with those of other cities, states, or countries. How do our schools "measure up?" What are the weaknesses? What can be done? This evaluation process is constant and continuing across the country.

In certain periods this examination is more intense. When the Soviet Union launched its Sputnik satellite in 1957, a great debate across the United States started. Was America "falling behind" in science and technology and in "the space race?" How did American school children compare in mathematics and foreign languages? This led to a massive investment in science education as well as to a search for, and support of, gifted pupils. The Civil Rights movement, too, had a shock effect on American education, all the way from pre-school programs to post-doctoral studies. Billions of dollars were made available for special programs for the educationally disadvantaged, for bilingual education, and for seeing minority students better represented in higher education. In the 1980s and into the '90s, again, America was swept by a great public debate over the quality, content, and goals of education.

Summing up results is extremely difficult. There are, for instance, literally thousands of special programs and hundreds of experimental schools across the nation. Since 1968 alone, Native American tribes have established 24 colleges of their own, mostly two-year institutions. In 1991, a survey of programs offering literacy instruction to linguistic minority students had 600 different programs return a questionnaire. Of these programs, all but 10 had been started since 1980. School "choice" approaches - allowing parents more freedom in determining which public, or, in some cases, private schools their children can attend - have been started in many districts. And, as another example, many areas have started "magnet" schools. These offer special curricula, perhaps an emphasis on science, mathematics, or even dance, and attract, and motivate, students.

Given America’s history and that of its people, their many backgrounds, needs, and desires, the fact that American education is sensitive to its weaknesses (and aware of its strengths) speaks well for the future.

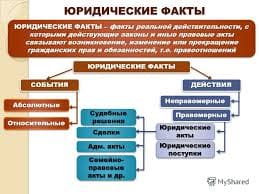
THE FACULTY OF MATHEMATICS

Numbers

It has been customary ever since Euclid’s time to present geometry in the form of an axiomatic system. Some other, different approaches to geometry have been developed by mo­dern mathematicians, but this axiomatic approach has conti­nued to be widely used and presented to beginners.

Our mathematics of numbers, however, has not traditionally been organized in axiomatic form. Arithmetic, school algebra, and such subjects as the differential and integral calculus (which go under the heading of analysis) have customarily been pre­sented as collections of rules of calculation, rather than in the form of axiomatized systems of laws.

This difference arises from the fact that our modern mathematics of numbers has its origins more in the mathematics of the Babylonians, Hindus, and Arabs than in that of the Greeks. The Greeks did treat some numerical problems, to be sure, but in doing so their method was to give geometrical interpretations to numbers; that is, when dealing with a problem about the comparative size of two numbers, they would treat it as a problem about the comparative lengths of two lines or the comparative areas of two figures.

But the Babylonians, Hindus, and Arabs (to whom we owe the word “algebra”) gradually developed sym­bols and rules of calculation that made it possible to deal with numerical problems more abstractly and more powerfully than could the Greeks. As was typical in Eastern mathematics, however, the Babylonians, Hindus, and Arabs did not much concern themselves with giving proofs, let alone with organizing their knowledge of numbers into axiomatic form.

Thus it happened that while geometry was being handed down¹ through medieval and early modern times in the axiomatized form which Euclid had given it, the mathematics of number was passed along² as a collection of comparatively unconnec­ted laws and rules of calculation. This situation is finally changing; one of the striking features of twentieth-century mathematics is its greatly increased use of the axiomatic approach in mathematical studies besides geometry.

From very early times, the development of the mathematics of number must have given rise to philosophical puzzlement. The whole numbers 1, 2, 3, etc. are not too disturbing, to be sure, for their legitimacy seems clear to us as we count the number of beasts in a herd or of kings in a dynasty. The fractions also are not too disturbing, for we can regard them clients of whole numbers, useful for comparing the sizes of fields or lengths of time.

But one can imagine that there have been difficulties when the Babylonians, wishing to express the result of subtracting a number from itself, introduced a symbol for zero, and eventually began to treat it just as through zero were one of the whole numbers. Zero seems like an emptiness, like nothing; how then can we legitimately refer to zero as though it were something, a genuine number? No doubt this uneasiness was gradually soothed ³ as people came to realize that zero is just for “counting”, the number of beasts in an empty field, or the number of kings during a republican era.

The introduction of symbols for negative numbers must have been a further source of difficulties, however; negative numbers seem somehow to be numbers that are not there, unreal ghosts of numbers – so is it legitimate to call them numbers? In modern times the introduction of symbols for imaginary numbers excited similar doubts. Even if we admit the legitimacy of talk about negative numbers, is it correct to speak of the square root of minus one as if it were a number? Wouldn't it be more honest just to say that minus one has no square root?

Philosophical puzzlement about the various kinds of numbers was much reduced⁴ thanks to the work of nineteenth century mathematicians who developed a unified theory of numbers. Their very important achievement consisted in showing how the mathematical theories concerning more sophisticated kinds of numbers can be “reduced to”, “constructed from”, a theory concerning only the basic kind of numbers. That is, they showed how each of the more sophisticated kinds of number, together with the operations (such as addition and multiplication) performable on numbers of that kind, can be defined in terms of the whole numbers and the operations performable upon them. They showed that this can be done in such a way that the laws which govern these more sophisticated kinds of numbers can then be deduced from the laws that govern the numbers.

This development is called the arithmetization analysis, because it is concerned with showing how those parts of mathematics that go under the heading of analysis, can be reduced to the elementary part of arithmetic (or elementary number theory, as it is called), when that is supplemented by certain notions that we shall mention.

This unified theory of numbers enables us to regard the various kinds of numbers as belonging to a single family, all springing from a single parent kind and all governed by laws that are strict deductive consequences of the laws governing that simple parent kind. If we accept this unified theory of numbers, we no longer need feel any special doubts about the more sophisticated kinds of number; any doubts that remain will be focused solely upon the numbers of the kind used in counting.

The numbers 0, 1, 2, 3, etc., will serve as our basic kind of numbers; they are called natural numbers (unfortunately that term has a slight ambiguity, for some writers include zero among the natural numbers while others do not but let us count it in). Now, our intuitive idea of the natural numbers is that they are all those numbers, each of which can be reached by starting from zero and adding one as often as necessary.

The Italian mathematician Peano was the first to organize the fundamental laws of these numbers in axiomatic form; his set of five axioms is notable. Let us consider these axioms so that we can feel more at home with the natural numbers before we go on to see how other kinds of number can be reduced to them. Expressed in words, Peano's axioms are:

1) Zero is a natural number.

2) The immediate successor ⁵ of any natural number is a natural number.

3) Distinct natural numbers never have the same immediate successor.

4) Zero is not the immediate successor of any natural number.

5) If something holds true of zero, and if, whenever it holds true of a natural number, it also holds true of the imme­diate successor of that natural number, then it holds true of all natural numbers.

These axioms contain three undefined terms: “zero”, “ immediate successor”, and “natural number”. The axioms by themselves do not show us what these terms are supposed to mean (though they do connect together whatever meanings these terms may have), nor do they give us any evidence that the terms do refer to anything real.

If we wish to accept the axioms as true we must supply that understanding and that evidence for ourselves. Underlying the use of these terms in the axioms are the tacit assumptions that “zero” does refer to some one definite entity among those under discussion, and that for each entity among those under discussion there is just one entity among them that is its immediate successor.

It fol­lows from the axioms that the immediate successor of zero, its immediate successor, and so on and on, all are natural num­bers; and (by the fifth axiom) that nothing else is a natural number. From the axioms it follows that there must be infini­tely many natural numbers, since the series cannot stop, nor can it circle back to its starting point (because zero is not the immediate successor of any natural number).

The fifth axiom is especially important, for it expresses the assumption which underlies mathematical induction. We can picture how reasoning by mathematical induction works if we imagine a series of dominoes standing in a row. Suppose we know that the first domino will fall and that whenever any domino falls the adjoining one also will fall; then we are entitled to infer that all the dominoes will fall; no matter how many there may be.

In the same spirit, if we know that something holds true of zero and that whenever it holds true of a natural number it also holds true of the immediate succes­sor of that natural number, then we can infer that it holds true of every natural number. On the basis of Peano's axioms, we can introduce the names of further numbers: “one” by definition names the immediate successor of zero, “two” by definition names the immediate successor of one, and so on.

Peano’s axioms express in a very clear way the essential principles about the natural numbers. However, they do not by themselves constitute a sufficient basis to permit the reductions of other higher kinds of numbers – assuming, that is, that we continue to restrict ourselves to the same compara­tively low-level logical principles that are employed for deducing theorems in geometry. There are two reasons for this.

For one thing, Peano’s axioms, do not by themselves provide us even with a complete theory of the natural numbers. If we limit ourselves just to Peano's three primitive terms and to his five axioms, it is impossible for us (using only normal low-level logical principles) to define addition and multiplication in their general sense for these numbers.

So we could not even express within the system, let alone prove within it, such laws as that the sum of natural numbers x and y always is the same number as the sum of y and x, or that x times the sum of y and z always is the same number as the sum of x times y and x times z. We do not even worry about subtraction and division, since these are not operations freely performable on the natural numbers.

Furthermore, in order to carry out this reduction of higher kinds of number we need to employ two other very important terms, “ set ” and “ ordered pair ”, which Peano of course did not include among his primitives.

Notes

1. while geometry was being handed down – в то время как геометрия дошла

2. the mathematics of number was passed along – математика числа пришла к нам в виде

3. this uneasiness was gradually soothed – это неудобство по­степенно сгладилось

4. philosophical puzzlement... was much reduced – философские сомнения... были в основном разрешены

5. the immediate successor – непосредственный последующий элемент

THE FACULTY OF BIOLOGY