Суммарное поле, создаваемое всеми зонами Френеля можно определить, если просуммировать волны, создаваемые элементами поверхности dS, находящимися в пределах каждой зоны в отдельности, а затем найти суммарное поле, обусловленное всеми зонами Френеля.
Если разделить каждую зону Френеля на некоторое число равных по площади концентрических колец, то эти волны, создаваемые каждым кольцом не будут отличаться друг от друга по амплитуде так как АВ>>λ. будут отличаться только по фазе.
Например, если первую зону Френеля разделить на 10 колец то фазы колебаний источников двух соседних колец будут отличатся друг от друга на 18о.
Геометрическое сложение колебаний можно изобразить в виде векторной диаграммы, а результирующий вектор для I зоны обозначить 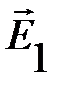 (рис., а)
(рис., а)
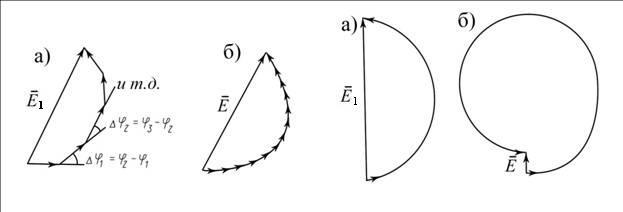
Рисунок 1 Рисунок 2
Рисунок 1- Векторное суммирование полей от различных участков отверстия: а) при скачкообразном, б) при плавном изменении его диаметра
Рисунок 2 - Векторное диаграмма при диаметре отверстия, соответствующим: а) первой зоне Френеля, б) второй зоне Френеля
Если приращение от кольца к кольцу невелико, то можно вместо ломанной линии получить плавную (рис., а).
Результирующий вектор второй зоны Френеля 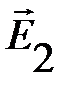 будет направлен противоположно
будет направлен противоположно 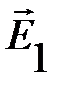 и по длине будет короче, вследствие увеличения расстояний АДn и ДnВ то есть
и по длине будет короче, вследствие увеличения расстояний АДn и ДnВ то есть 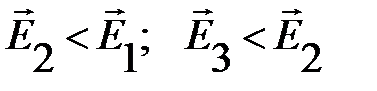 и т.д. и разность фаз будет равна 180о.
и т.д. и разность фаз будет равна 180о.
Суммирование можно представить в виде скручивающейся спирали. Отрезок между началом А и концом стрелки показывает величину результирующего колебания при перемещении по спирали. При приближении к фокусу спирали результирующая амплитуда колебания приближается к 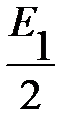 (рис).
(рис).
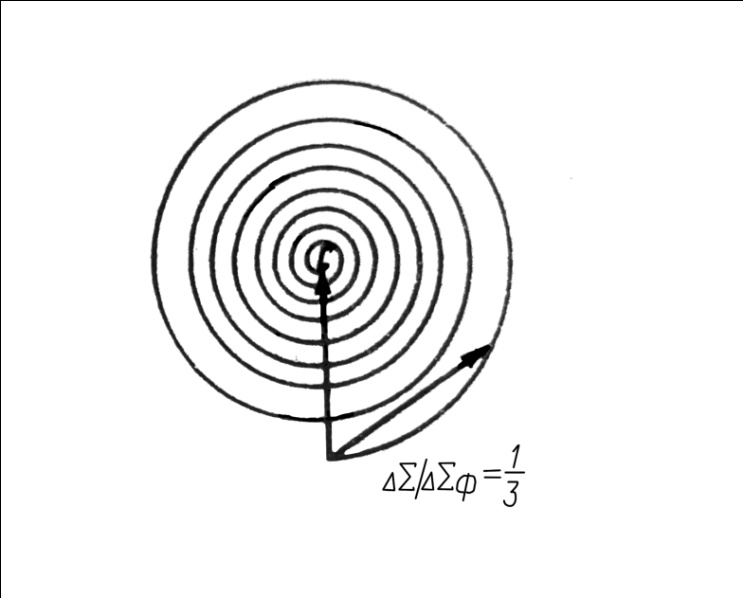
Рисунок - Векторная диаграмма при увеличении диаметра отверстия до бесконечных размеров
Так как фазы соседних зон отличаются на 180о и векторы 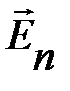 коллинеарны, то геометрическое суммирование сводится к алгебраическому.
коллинеарны, то геометрическое суммирование сводится к алгебраическому.
Разделение плоскости S на зоны Френеля дает возможность представить результирующую амплитуду волн вторичных источников всех зон в виде знакопеременного сходящегося ряда
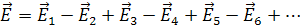 ()
()
Соседние члены этого ряда мало отличаются друг от друга и поэтому каждый из членов можно считать равным среднему арифметическому из двух соседних членов. Тогда ряд записывается
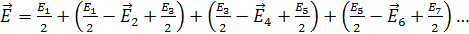 ()
()
При 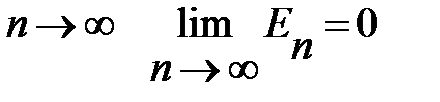 , то величина в скобках близка нулю, то тогда результирующий вектор
, то величина в скобках близка нулю, то тогда результирующий вектор 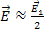 , то есть половине значения напряженности поля, создаваемой первой зоной Френеля. Другая половина
, то есть половине значения напряженности поля, создаваемой первой зоной Френеля. Другая половина 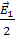 , а также поля, создаваемые зонами Френеля высших номеров компенсируются взаимно.
, а также поля, создаваемые зонами Френеля высших номеров компенсируются взаимно.
Графически можно представить результат в виде осциллирующей кривой (рис.).
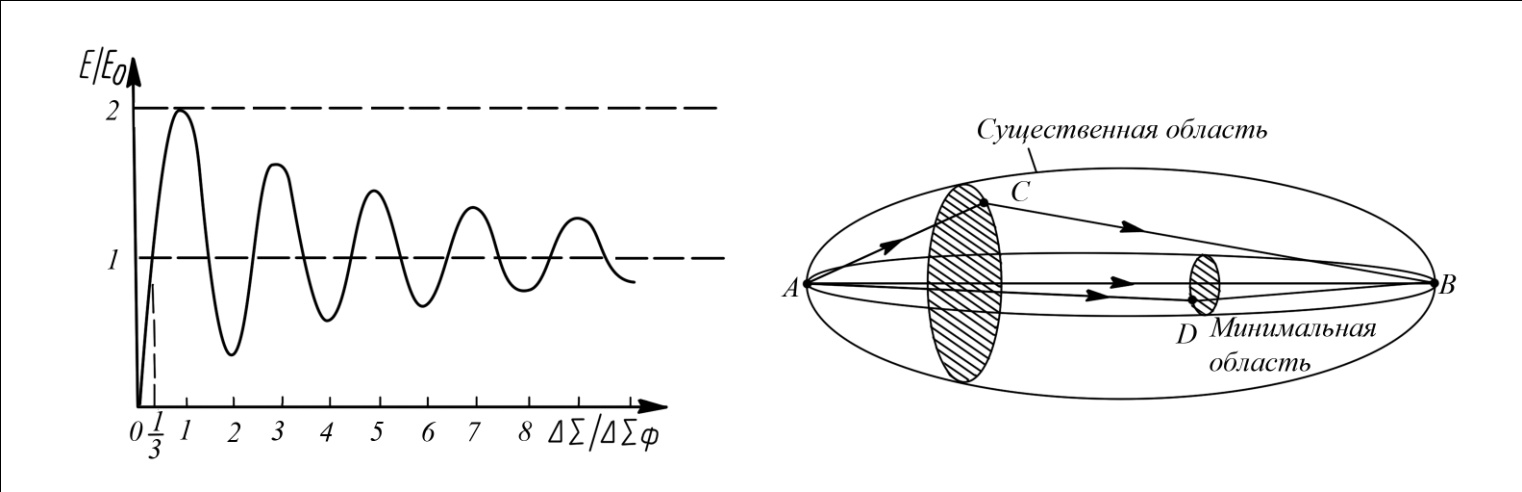
Рисунок - Зависимость 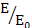 от радиуса зон Френеля
от радиуса зон Френеля
Таким образом результирующее поле в точке наблюдения в основном создается волнами вторичных излучателей, расположенными в пределах первых нескольких зон Френеля (n=6-8 зон). Вклад остальных зон очень мал, в силу быстрой сходимости ряда ().
Размеры зон Френеля.
Определим радиусы зон Френеля. Обозначим ρn радиус n-зоны. Геометрия задачи представлена на рисунке
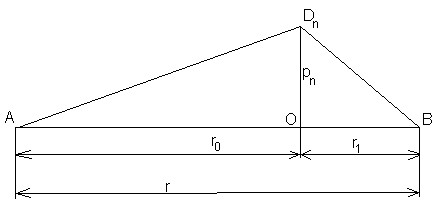
Рисунок - Определение радиусов зон Френеля
Из рисунка () из простых геометрических соображений находим:
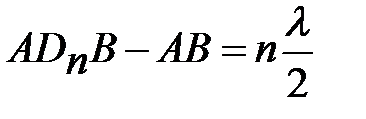
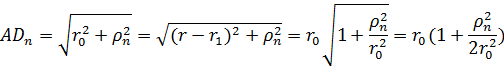 Из
Из 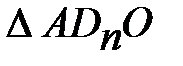 :
:
()
Учитывая, что на практике всегда выполняются условия что r0>>λ и r1>>λ, то радикал в уравнении () можно разложить биноминальный ряд вида
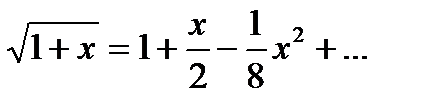
Так как x<<1 то в этом разложении берем первых два члена, тогда 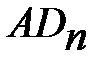 из () будет равно
из () будет равно
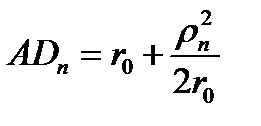 ()
()
Из 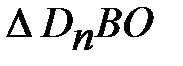 :
:
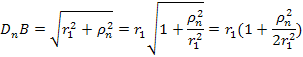
Аналогично определению 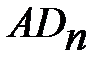
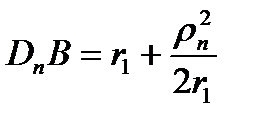 ()
()
Используя условие 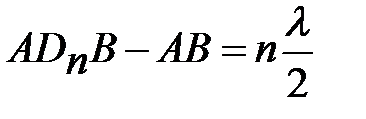 , получаем уравнение для определения радиуса n-ой зоны Френеля
, получаем уравнение для определения радиуса n-ой зоны Френеля
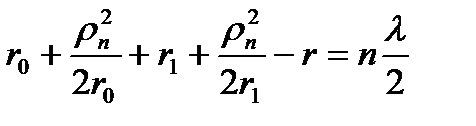
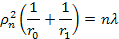
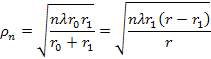
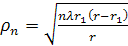 ()
()
Первая зона Френеля – круг с радиусом 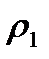 достигает максимального значения на середине трассы.
достигает максимального значения на середине трассы.
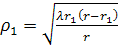 , ()
, ()
а зоны Френеля с номером 2 и более – кольца, внешний радиус которых определяется ().
Площади всех зон Френеля одинаковы и имеют величину
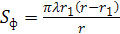 . ()
. ()
Если 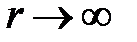 , а r1 – остается конечным, то
, а r1 – остается конечным, то
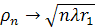
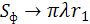
 2015-06-24
2015-06-24 1491
1491








