В 1857 году ирландский математик предложил У. Гамильтон предложил игру, названную «Кругосветное путешествие/путешествие по додекаэдру». Игра сводилась к обходу по рёбрам по рёбрам всех вершин правильного додекаэдра, при условии, что нужно обойти все вершины ровно по одному разу и вернуться в исходную точку. Додекаэдр – это правильный (платонов) многогранник, гранями которого служат 12 правильных пятиугольников. У него 20 вершин и 30 рёбер. В каждой его вершине сходятся по 3 ребра (регулярный граф). Плоское изображение графа показано на рисунке.
1, 2, 3, 4, 5, 6, 19, 18, 14, 15, 16, 17, 7, 8, 9, 10, 11, 12, 13, 20.
К этому же типу задач относится задача об оптимальном маршруте на выставке, в которой требуется посетить каждый зал ровно один раз. Метрополитен?
Если граф имеет простой цикл, содержащий все вершины графа (по одному разу), то такой цикл называется гамильтоновымциклом, а граф называется гамильтоновым графом.
Поиск критерия гамильтоновости графа – одна из основных нерешённых проблем теории графов. О гамильтоновых графах известно ещё очень мало.
Необходимые условия гамильтоновости графа неизвестны. Ясно, что гамильтонов граф должен быть связным. Ясно, что гамильтонов цикл не обязательно содержит все рёбра графа; гамильтонов путь всегда простой. Известны только некоторые достаточные условия – так, полный граф всегда гамильтонов. Чем больше степень каждой вершины тем, очевидно, вероятней существование гамильтонова пути. Один из наиболее известных результатов общего характера предлагается в такой теореме.
Теорема Дирака. Если в графе G = <V, E> с n ³ 3 вершинами deg(vi) ³ n/2,то граф G является гамильтоновым.
Поиск гамильтонова цикла в графе является одной из классических задач теории графов и теории алгоритмов. Решить её можно следующим образом. Если в графе G = <V, E> с n вершинами зафиксировать одну из вершин и обход графа всегда начинать с неё, то всякому гамильтоновому циклу будет соответствовать перестановка множества вершин (v1, v(i1), …, v(in-1)). Следовательно, найти гамильтонов цикл или убедиться в его отсутствии можно путём перебора (n-1)! перестановок. Если граф гамильтонов, то этот перебор в полном необходимо будет выполнить лишь в случае большого невезения, т.е. когда перестановка, соответствующая гамильтонову циклу, встретится в этом процессе последней. Если же граф негамильтонов или необходимо найти все гамильтоновы циклы, то, действуя таким образом, необходимо перебрать все (n-1)! перестановок. Хотя на практике пользуются разными алгоритмами частичного перебора, но всё равно сложность этих алгоритмов остаётся высокой – пропорциональной (n-1)!
Для примера: нахождение гамильтонова цикла в графе, содержащем 14 вершин, требует суточной работы самых мощных машин; увеличение быстродействия в 10 раз приведет к решению в сутки задачи с 15-ю городами; для 50 городов потребуется ~109 лет.
Существует класс так называемых переборных задач, сложность которых аналогична задаче Гамильтона. Если хотя бы для одной из этих задач существует эффективный алгоритм[1], то также существует эффективный алгоритм решения целого класса аналогичных задач – так называемых NP-полных задач. Верно и обратное – доказательство отсутствия эффективного алгоритма для одной задачи распространяется на весь класс. На этом основано общепринятое мнение, что таких алгоритмов не существует.
Задача коммивояжёра формулируется следующим образом.
Имеется n городов, расстояния между которыми известны. Коммивояжёр должен посетить все n городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут, при котором суммарное пройденное расстояние (стоимость/надёжность пути) будет минимальным.
Задача коммивояжёра состоит из 2-х частей – сначала надо найти все гамильтоновы циклы в графе, а затем для каждого найденного цикла вычислить вес и выбрать минимальный (максимальный). Практически следует рассматривать и варианты без возврата в начальную вершину.
Планарность графов
При введении понятия изоморфизма графов отмечалось, что возможно несколько изображений одного графа. На практике при изготовлении микросхем необходимо выяснить, можно ли схему электронного устройства, которая представляет собой граф, разместить на плоскости без пересечения проводников. Аналогичная задача возникает при проектировании железнодорожных и других путей, где нежелательны переезды. Таким образом, возникает задача изучения плоских графов – графов, которые могут быть нарисованы на плоскости без пересечения линий. Для строгого определения понятий «линия», «пересечение», «изобразить» и пр. нам необходимо совершить небольшой экскурс в соответствующий раздел математики.
Жордановой кривой на плоскости (на сфере, в пространстве, etc…) называется непрерывная кривая, не имеющая самопересечений. Замкнутой жордановой кривой называется жорданова кривая, начало и конец которой совпадают.

Рис. 1. Примеры жордановых кривых
Теорема Жордана. Пусть W – область, границей которой служит замкнутая жорданова кривая L, точки x, y Î L. Тогда: любая жорданова кривая Г, имеющая началом и концом точки x и y: а) лежит целиком в W; б) лежит целиком вне W; в) пересекает L в точках, отличных от x и y.
Определение. Граф G(V,E) обладает укладкой (может быть уложен) в данном пространстве, если он изоморфен некоторому графу, изображённому в этом пространстве при помощи точек, представляющих вершины V и жордановых кривых, представляющих рёбра E, причём эти жордановы кривые не пересекают друг друга.
Определение пересечения:
а) жордановы кривые, соответствующие разным рёбрам, пересекаются в точках, не соответствующих вершинам;
б) жорданова кривая, соответствующая ребру, проходит через вершину, не инцидентную ребру.
С меньшей строгостью: укладкой графа называется такое его геометрическое изображение, при котором ребра пересекаются только в вершинах.
Лемма. Любой граф может быть уложен в трехмерном пространстве.
◄ Рисуем вершины графа на прямой линии. Для любого ребра еi, соединяющего 2 вершины проводим плоскость, содержащую эту прямую, а ребро рисуем на плоскости. ►
Граф называется планарным, если существует его укладка на плоскости. Сама же укладка графа на плоскости называется плоским графом.
Граф планарен, если существует его укладка на сфере. Доказательство – стереографическая проекция.
Доказательство следует из взаимно однозначного соответствия точек на сфере с точками плоскости из стереографических проекций.
Следствие. Граф любого выпуклого многогранника планарен.
Ребра плоского графа разбивают плоскость на несколько частей, одна из которых бесконечна. Эти части и являются гранями плоского графа.
Теорема Эйлера (формула Эйлера ). В связном планарном графе справедливо следующее соотношение между числами вершин, ребер и граней:
В – Р + Г = 2, или n – m + g = 2.
Докажем индукцией по числу граней
►Если g = 1, то в графе нет ни одного цикла (такой граф называется деревом). У дерева число вершин больше числа ребер на 1, т.е. n = m + 1 ” n – (n–1) + 1 = 2 – формула справедлива.
Пусть формула Эйлера верна при g = k–1. Рассмотрим граф с числом граней g = k.
Возьмём ребро, отделяющее бесконечную грань от внутренних и удалим его из графа. Полученный граф останется связным (мы выбрали именно такое ребро) и будет иметь n вершин, m–1 ребро и k–1 грань. По предположению индукции n – (m–1) + (k–1) = 2, т.е. n–m+k=2. ◄
Следствие 1. Д ля плоского связного простого графа справедливо соотношение: n £ 3(m–2).
Следствие 2. Для плоского связного простого графа без треугольных граней справедливо соотношение: n £ 2(m–2).
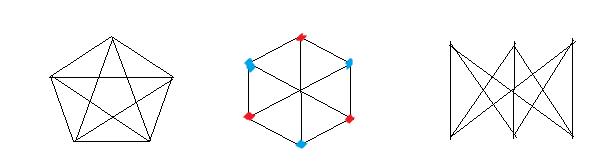
Граф К5 Изоморфизмы графа К3,3
Рис. 2. Непланарные графы
 2015-06-24
2015-06-24 4685
4685








