Шаг 1. Полагаем S=V\{v0}, d[vi] =a(v0, vi) для всех i=1,…,k.
Шаг 2. Если |S| = 1, то выполнить шаг 4. Выбрать в S элемент v*, для которого величина d[v*] является наименьшей (среди всех элементов из S).
Шаг 3. Положить S=S\{v*}, d[v] =min{d[v], d[v*]+d[v*®v]} "vÎS и перейти к шагу 2.
Шаг 4. Выдать d(v1),…,d(vk). Конец работы алгоритма.
Алгоритм осуществляет «итерративный» процесс нахождения расстояния d(vi) для i=1,…,k. Проследим, как это делается для сети N, изображенной на рис. 6.12. Работа алгоритма будет иллюстрироваться заполнением таблицы 6.1.
При выполнении первого шага алгоритма величины d(vi) примут значения, которые указаны в нулевой строке таблицы. Из них точным является только d(v2), значения остальных величин завышены. На шаге 2 в качестве v’ выбирается вершина v2 (в таблице соответствующее значение набрано жирным шрифтом) и удаляется из S на шаге 3. На том же шаге уточняются предыдущие значения d(v) для vÎS (см. первую строку таблицы 6.1). На этом первый проход алгоритма заканчивается. На втором проходе в качестве v’ берется v5, удаляется из S и значения d(v) для vÎS снова уточняются. Результат уточнения отражен во второй строке таблицы. Когда множество S будет содержать только вершину V3, алгоритм заканчивает работу. Результат: d(v1)=3, d(v2)=1, d(v3)=4, d(v4)=4, d(v5)=3.
|
|
|
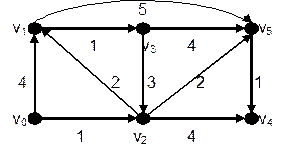
| Номер строки | d(v1) | d(v2) | d(v3) | d(v4) | d(v5) |
| ¥ | ¥ | ¥ | |||
| ¥ | |||||
| ¥ | |||||
Поскольку на каждом проходе алгоритма число элементов множества S уменьшается на единицу, то алгоритм Дейкстры всегда заканчивает работу. Следующее утверждение показывает, что он выдает «то что нужно».
Теорема. Пусть для сети N и фиксированной вершины v0 этой сети алгоритм Дейкстры выдал величины d(v1),…,d(vk). Тогда d(vi) есть расстояние от v0 до vi для i=1,…,k.
Доказательство. Отметим вначале, что если d(vi)¹ ¥, то величина d(vi) равна длине некоторого пути из v0 в vi. Пусть в очередном проходе алгоритма на втором шаге выбирается вершина v’, d(v’) ¹ ¥ и
v0=x0, x1,…,xi-1,xi,…,xp-1, xp=v’ –
кратчайший (v0,v’)–путь. Убедимся в том, что для любой вершины х этого пути выполняется равенство d(x)=d0(v0,x). Действительно, для х=х0 это справедливо. Предположим, что d(xi-1)=d(v0,x), но d(xi)>d(v0,xi). Тогда поскольку d(xi-1)<d(v’), то вершина хi-1 выбиралась на втором шаге в более раннем проходе алгоритма. На третьем шаге этого прохода d(xi) получило бы значение d(xi-1)+a(xi-1,xi), которое равно d(v0,xi). Следовательно, для любой вершины х фиксированного пути выполняется равенство d(x)=d(v0,x), в частности, d(v’)=d(v0,v’). Отсюда следует, что если существует (v0,v)–путь в сети N, то на момент завершения работы алгоритма выполняется равенство d(v)=d(v0,v).
|
|
|
 2015-06-24
2015-06-24 467
467








