Потоки в сетях

Будем рассматривать орграф как сеть труб (или дорог), по которым некое вещество движется от истока (где оно производится с постоянной скоростью) к стоку (где оно потребляется с той же скоростью). Каждому ребру графа в этом случае следует приписать число, характеризующее его пропускную способность (а не длину, стоимость, как это было раньше). Задача о максимальном потоке для данной сети состоит в следующем: найти максимально возможную скорость производства (и потребления) вещества, при которой его ещё можно доставить по данной сети.

Сетью называется ориентированный граф, каждому ребру (u,v)ÎE которого поставлено в соответствие число c(u,v), называемое пропускной способностью ребра. В графе выделены две вершины: исток s (source)и сток (sink) t.

Потоком в сети называется функция f: V´V a ¡, обладающая следующими свойствами.

1. 0≤ f (u,v)≤ c (u,v)

2. f (u,v)= – f (v,u)

3.

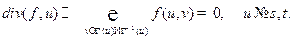
Величина потока определяется как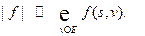

Всякий разрез сети Р определяется разбиением вершин на два подмножества S и T, а в Р попадают все рёбра, соединяющие S и T. Сумма потоков через рёбра разреза обозначается f(P), а сумма пропускных способностей рёбер разреза Р называется пропускной способностью разреза и обозначается с(Р):

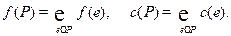
Основная задача о потоках в сетях: найти максимальный для данной сети поток. Такой поток называют пропускной способностью сети. Следующая теорема утверждает, что пропускную способность сети можно вычислить, не зная самого потока.

Теорема Форда – Фалкерсона. Максимальный поток в сети равен минимальной пропускной способности разреза.

Другими словами – через всю сеть (трубу) пройдёт столько же, сколько через самое узкое место. При доказательстве теоремы используется лемма:

Поток через любой разрез равен стоку. — Эта лемма в точности повторяет закон Гаусса: поток электрического поля через поверхность тела равен заряду, находящемуся внутри поверхности. И доказательство аналогично – дивергенция в узлах равна нулю, поэтому можно как угодно деформировать разрез.

Следствие: величина потока не превосходит пропускной способности разреза.

Вторая задача – найти максимальный поток.

Алгоритм построения максимального потока. Перераспределение потока.

Допустимым называется любой поток, удовлетворяющий условиям 1-3 (например, нулевой). Обозначим матрицу потока через F, матрицу пропускных способностей через С. Если поток не максимальный, его можно увеличить за счёт а) насыщения не насыщенных рёбер; б) уменьшения встречного потока («встречные перевозки»).

1. Построим матрицу остаточной пропускной способности рёбер R_F=C–F – соответствующая ей сеть называемую остаточной сетью; насыщенные рёбра в неё можно не включать.

2. Найдём в остаточной сети дополнительный путь (augmenting path) от истока к стоку. — Этот путь ищется алгоритмом фронта волны.— Если дополнительного пути не существует – максимальный поток построен* – конец алгоритма.

3. Добавим найденный дополнительный поток к предыдущему и повторим п.1.