Пример. Представим числа 0÷9 в двоичном виде: <0,1,10,11,…1001>. Такое кодирование однозначно, но декодирования нет: К(333) = 111111 = К(77). Ситуацию можно исправить, если в начальных разрядах дописать нули: 0→0000, …, 9→1001. Такое кодирование называется двоично-десятичным.
Префиксное кодирование. Никакое кодовое слово префиксного кода не является началом (префиксом) другого кодового слова.
Предположим, нам надо передать сообщения, записанные с помощью четырёх букв: а, б, в, г. Эти сообщения можно закодировать так, как показано во второй строчке таблицы:
| кодирование\сообщения | а | б | в | г | цена кодирования |
| равномерное | |||||
| разделимое, префиксное | 1,75 | ||||
| неразделимое | 1,25 | ||||
| частота | 0,5 | 0,25 | 0,125 | 0,125 |
При равномерном кодировании не учитывается вероятность появления букв, или предполагается одинаковой для всех четырёх сообщений. Между тем появление их в информационном тексте может происходить с различной частотой – в этом случае выгодно назначить короткие кодовые слова наиболее часто появляющимся буквам, а длинные коды – редко встречающимся.
|
|
|
Принцип оптимизации кода следующий. Если задана схема кодирования К = <ai →bi, i=1,…,n>, то схема К′ = <ai →b′i, i=1,…,n>, где b′i являются некоторыми перестановками bi, также будет кодированием. Если длины элементарных кодов равны, то длина кода сообщения от такой перестановки не изменится. Но если длины кодов разные, то длина кода сообщения будет зависеть от состава букв в сообщении и от того, какие элементарные коды буквам назначены. Если отсортировать буквы по частоте их вхождения в сообщение, а коды по длине, и сопоставить соответствующие списки, то можно минимизировать длину кода сообщения. Очевидно, что найденное соответствие не будет минимизировать все тексты. Но, для естественных языков известны вероятности (частоты) появления каждой буквы. Поэтому достаточно большие тексты минимизируются в соответствии с принципом: большей частоте – меньшую длину.
Принцип кодирования Фано следующий. Все сообщения (буквы) выписываются в таблицу по степени убывания вероятностей и разбиваются на две группы равной (насколько это возможно) вероятности (медиана). Первой группе присваивается 0, второй группе – 1. Затем каждая группа вновь делится на две подгруппы равной вероятности (квартили), которым также присваиваются символы 0 и 1. В результате многократного повторения этой процедуры получается таблица кодовых слов. В нашем примере схема Фано задаётся третьей строчкой таблицы.
Показателем экономичности кода служит средняя длина кодового слова, которая называется ценой кодирования и определяется как математическое ожидание 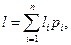 где l i = | b i| – длина кодового слова ai, p i – вероятность появления ai, n – число букв в алфавите А.
где l i = | b i| – длина кодового слова ai, p i – вероятность появления ai, n – число букв в алфавите А.
|
|
|
В рассмотренном примере цена равномерного кодирования равна 2, кодирования Фано – 1, 75. На первый взгляд, кодирование по Фано кажется избыточным, поскольку можно кодировать так, как записано в 4–й строчке таблицы, и получить цену 1,25.
Наряду с методом Фано, существует кодирование по методу Хаффмана. Принцип Хаффмана – объединение двух букв с наименьшей вероятностью, сортировка. Это продолжается до тех пор, пока не останется 2 строчки. Пишем одной 0, второй 1. Идём по таблице назад.
Бинарное дерево сортировки.
Для разобранного примера коды Фано и Хаффмана совпадают, но в общем случае кодирование Фано уступает в экономичности кодированию Хаффмана. Более того, Хаффман показал, что его кодирование даёт предельное сжатие информационного текста. Это оптимальное кодирование или кодирование с минимальной избыточностью.
Возьмём следующий закодированный текст: 00101000. Согласно последней строчке, данный текст не может быть однозначно дешифрован, так как непонятно, что подразумевается: сообщения вида – бввгб; или – гавббб, или – ббабабг и т.д. Расшифровка же текста по третьей строчке производится однозначно – вбг. (авба) Из-за этого замечательного свойства коды Фано и Хаффмена называют префиксным. Никакое кодовое слово префиксного кода не является началом (префиксом) другого кодового слова.
Коды Фано и Хаффмана – это частный случай разделимых кодов. Схема кодирования К называется разделимой, если кодовые сообщения обладают свойством:
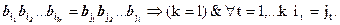
Т.е., в разделимой схеме любое кодовое сообщение единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой однозначно декодируется.
Замечание: равномерное кодирование является разделимой схемой, если К является инъекцией, т.е. все коды различны.
Теорема. Если схема К = < ai→bi, i=1,…,n> разделима, то длины слов удовлетворяют
неравенству Макмиллана: 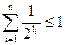 , где li = | bi |.
, где li = | bi |.
Это необходимое условие разделимости схемы кодирования. Неравенство Макмиллана является в то же время и достаточным условием разделимости, что утверждает следующая
Теорема. Если набор l 1, …, l n, l i = | b i| удовлетворяет неравенству Макмиллана 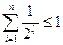 , то существует разделимая схема Σ = < ai→bi, i=1,…,n>, в которой | bi | = l i.
, то существует разделимая схема Σ = < ai→bi, i=1,…,n>, в которой | bi | = l i.
Замечание. Азбука Морзе – не разделимая схема – если не учитывать пауз между буквами и словами.
Замечание. Самым экономичным является кодирование тремя символами – (0, 1, 2).
Схема оптимального кодирования – если известны вероятности появления букв P = <p1,…pn>, то можно вычислить математическое ожидание длины кода, называемое ценой кодирования: 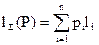 , li = | bi |. Оптимальным кодированием называется
, li = | bi |. Оптимальным кодированием называется 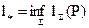 .
.
Лемма. Пусть Σ = <ai →bi, i=1,…,n> - схема оптимального кодирования для распределения вероятностей p1≥ p2≥…≥ pn>0. Тогда, если pi > pj, то li ≤ lj.
 2015-06-24
2015-06-24 3597
3597
