При передаче сообщения его можно кодировать как целиком, так и разделив на части. В этом случае кодирование K можно задать схемой, или таблицей кодов K = <a1→b1, a2→b2, …,an→bn>, сопоставляющей словам из A+ слова из В *. Например, можно взять «Толковый словарь живаго великорусскаго языка» В.И. Даля и занумеровать каждое слово. Русские слова тогда будут закодированы арабскими числами.
Распространённый способ кодирования – когда выбирается некоторый фиксированный набор «элементарных» слов из языка L и они кодируются. При этом, разумеется, все слова языка L должны записываться через набор элементарных слов. Множество кодов элементарных слов { bi } = { K(ai) } Ì B* называется множеством элементарных кодов. Например, в качестве элементарных слов можно взять слоги определённой длины (слоговое письмо). В простейшем случае кодированию подвергается каждая буква сообщения, т.е. в схеме кодирования ak – это символы алфавита – буквы, знаки препинания, цифры, пробелы. Такое кодирование называется алфавитным кодированием и полностью задаётся схемой (или таблицей кодов) – соответствий между буквами алфавита А и словами в алфавите В*:
К = <a1→ b1, a2→ b2, …,an→ bn >.
Пример алфавитного кодирования – ASCII коды.
Алфавитное кодирование пригодно для любого множества сообщений S.
Пример «слогового» кодирования – закодируем ASCII коды словами большей длины, например 16-ти битными, 32, …
Если элементарные коды имеют одинаковую длину, |bi| = n, то такое кодирование называется равномерным кодированием. Если вдобавок и элементарные слова имеют постоянную длину, то такое кодирование называется равномерным (m,n)-кодированием. Так, предыдущее предложение дало бы (8,16), (8, 32) равномерные коды.
Зачем нужно кодирование, в котором n>m? Дело в том, что при передаче данных по каналу связи всегда есть ненулевая вероятность ошибки. Так, для двоичного кодирования при передаче данных могут возникнуть ошибки следующих типов:
· 0→1, 1→ 0 – ошибка замещения разряда;
· 0→l, 1→l – ошибка выпадения разряда;
· l→0, l→1 – ошибка вставки разряда.
Канал характеризуется верхней оценкой количества ошибок каждого типа, возможных при передаче сообщения длины n: δ = <n1,n2,n3>.
Для защиты передаваемых текстов от помех информации от помех используются информационная избыточность, которая позволяет найти и исправить ошибки в данных. Такие коды называются корректирующими.
Корректирующие коды делятся на два класса:
а) коды с обнаружением ошибок;
б) коды с исправлением ошибок.
Самый простой способ создания избыточности достигается многократным дублированием передаваемых символов, т.е. образованием символьных блоков: (0®00, 1®11) или (0®000, 1®111). В первом случае, если произошла однократная ошибка, на выходе из канала связи появятся слова 01 или 10 – сигнализирующие об ошибке. Следовательно, это кодирование с обнаружением однократной ошибки.
Во втором случае (см. граф булева куба) однократную ошибку можно не только обнаружить, но и исправить. – В случае сбоя, решение по дешифровке принимается по большинству оставшихся однотипных символов в блоке (функция голосования).
Сами блоки могут включать в себя большее чем 3 число символов, тогда степень защищённости текста окажется выше. Если длину блока выбрать заранее достаточно большой, то практически любые ошибки можно исключить, правда, при этом скорость передачи информации упадёт пропорционально количеству символов в блоке – и возрастёт вероятность ошибки. Поэтому приходится искать компромисс между надёжностью и длиной (избыточностью) кода.
Очевидно, что для увеличения помехозащищённости кода – способности исправлять несколько ошибок – необходимо, чтобы элементарные коды отличались между собой как можно больше. Характеристикой различия слов служит расстояние Хэмминга: d(a, b) – число несовпадающих букв в словах a и b. Расстояние Хэмминга удовлетворяет обычным аксиомам расстояния:
А1. d(a, b) ≥ 0, причём d(a, b) = 0 только при a = b;
А2. d(a, b) = d(b, a);
А3. d(a, b) + d(b, c) = d(a, c) – неравенство треугольника.
Теорема 1. Для того чтобы код позволял обнаруживать ошибку не менее чем в q позициях, необходимо и достаточно, чтобы для всех пар кодовых слов выполнялось неравенство:
min(d(bi, bj)) ≥ q + 1.
Теорема 2. Для того чтобы код позволял исправлять ошибки не менее чем в q позициях, необходимо и достаточно, чтобы для всех пар кодовых слов выполнялось неравенство:
min(d(bi, bj)) ≥ 2q + 1.
Так, код (m, m+1) с проверкой по чётности имеет min(d(bi, bj)) =2, код (m,2m) тоже имеет min(d(bi, bj)) =2, а для кода (m,3m) с тройным повторением min(d(bi, bj)) = 3. (См. булев куб.)
Существует очень простая, но эффективная защита информационного текста от одиночной ошибки, которая требует минимальной избыточности в один символ. Это – проверка на чётность. При кодировании к каждому слову добавляется один разряд, который заносится 0 или 1 – в зависимости от чётности или нечётности суммы единиц в самом слове. Следовательно, это код типа (m, m+1): в кодовое слово записывается исходное сообщение длины m, в дополнительный разряд записывается 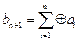 (сумма по модулю 2 всех предыдущих – информационных – разрядов). В приемном канале вычисляется сумма всех разрядов:
(сумма по модулю 2 всех предыдущих – информационных – разрядов). В приемном канале вычисляется сумма всех разрядов: 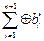 . При правильной передаче она должна быть равна 0, при замещении одного разряда – 1, при замещении двух – снова нулю и т.д. Если вероятность однократной ошибки мала, схема достаточно эффективна. Если при приёме обнаруживается нечётное число единиц, система регистрирует сбой и информация пересылается повторно. Контроль по чётности осуществляется в оперативной памяти компьютера.
. При правильной передаче она должна быть равна 0, при замещении одного разряда – 1, при замещении двух – снова нулю и т.д. Если вероятность однократной ошибки мала, схема достаточно эффективна. Если при приёме обнаруживается нечётное число единиц, система регистрирует сбой и информация пересылается повторно. Контроль по чётности осуществляется в оперативной памяти компьютера.
Обобщая эту идею, можно зарезервировать несколько контрольных разрядов, в которых можно заложить дополнительную информацию. Кодовое слово в этом случае будет представлять собой m информационных разрядов, в которых записывается исходное слово, и k = n – m контрольных разрядов, в которых находится информация, позволяющая контролировать правильность передачи сообщения (и корректировать его при необходимости). Кодирование в этом случае описывается схемой:
a = (a1,a2,…,am) → b = (a1,a2,…,am,c1,c2,…,ck),
в которой контрольные разряды вычисляются определённым образом по информационным.
Таблицу кодов в данном случае можно записать в матричном виде: b = a G, где G – блочная булева m 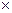 n матрица вида
n матрица вида 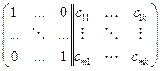 . Матричное умножение осуществляется по правилам булевой алгебры – логическое умножение (конъюнкция) и сумма по модулю 2. Так, дополнительные разряды можно вычислить через коэффициенты матрицы по формуле
. Матричное умножение осуществляется по правилам булевой алгебры – логическое умножение (конъюнкция) и сумма по модулю 2. Так, дополнительные разряды можно вычислить через коэффициенты матрицы по формуле 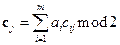 . Это разновидность матричного кодирования.
. Это разновидность матричного кодирования.
В данной схеме кодирования в элементарном коде первые m разрядов (их называют информационными) просто совпадают с исходным словом, в последних k = n–m разрядах можно поместить дополнительную информацию (эти разряды называют контрольными).
Вообще говоря, нет надобности ставить контрольные разряды в конце кодового слова – их можно разместить в любом месте. В этом случае матрица G будет не блочно диагональной, а общего вида:
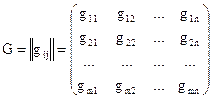 .
.
Такое кодирование называется матричным. Для декодирования следует задать обратную функцию D:{0,1}n→{0,1)m. Матрица G называется порождающейматрицей кода. При матричном кодировании, помимо порождающей матрицы кода G задают проверочную матрицу Н, удовлетворяющую условию GHT = (HGT) T = 0.
Кодирование в развёрнутом виде задаётся формулой 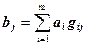 . Принятое сообщение проверяется проверочной матрицей: bHT = e, где е – слово длины k. Если сообщение принято без искажений, то е = 0. Если же в процессе передачи данных произошли искажения, то слово е ¹ 0 и, в принципе, несёт информацию, позволяющую определить, в каком разряде произошёл сбой и исправить этот разряд.
. Принятое сообщение проверяется проверочной матрицей: bHT = e, где е – слово длины k. Если сообщение принято без искажений, то е = 0. Если же в процессе передачи данных произошли искажения, то слово е ¹ 0 и, в принципе, несёт информацию, позволяющую определить, в каком разряде произошёл сбой и исправить этот разряд.
На матричном языке рассмотренные примеры выглядят следующим образом.
Например, при (1, 3) кодировании имеем 0 → 000, 1→111, или 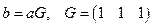 , или
, или 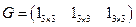 для (3,9) кодирования. В этом случае функция голосования
для (3,9) кодирования. В этом случае функция голосования 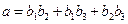 даёт правильный ответ при однократном сбое (и без оного).
даёт правильный ответ при однократном сбое (и без оного).
Пример: По рзелуьаттам илссеовадний одонго анлигйсокго унвиертисета, не иеемт занчнеия, в кокам пряокде рсапожолены бкувы в солве. Галвоне, чотбы преавя и пслоендяя бквуы блыи на мсете. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, всё рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы не чиатем кдаужю бвуку по отдльенотси, а всё солво цликеом
Существуют различные виды матричного кодирования: групповые коды Х эмминга, циклические коды, линейные, именные и т.д. Эти коды применяются для исправления ошибок при передаче данных по внутренним шинам компьютера, в оперативную память, на периферию и т.п.
Одним из классов групповых кодов, исправляющих однократную ошибку типа замещения, являются групповые коды Хэмминга. Для того чтобы код Хэмминга исправлял однократную ошибку в слове длины n (например, внутренние шины компьютера), необходимо выполнение неравенства 2k ≥ n+1 или 2n/(n+1) ≥ 2m. Так, при m = 32 необходимо k = 6 контрольных разрядов. Коды Хэмминга: (1, 3), (4, 7), (11, 15) и т.д. строятся по фундаментальным решениям систем уравнений b HT, где H – матрицы порядка k 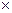 2k–1 (= k
2k–1 (= k 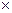 n), представляющих из себя последовательную запись по столбцам чисел 1, …, 2k–1.
n), представляющих из себя последовательную запись по столбцам чисел 1, …, 2k–1.
Принцип построения кода Хэмминга следующий. Кодовое слово b представляет из себя набор m информационных и k контрольных разрядов: b = (a1,a2,…,am,c1,c2,…,ck), но контрольные разряды расположены среди информационных в определённом порядке. Так как длина кодового слова больше, чем информационного, на кодовое слово можно дополнительно наложить k условий. В матричном виде это будет условие bH T= 0, где проверочная матрица H имеет размер k‰n. Если в процессе передачи данных произошло искажение (в одном разряде), то в правой части этого выражения появится некоторый вектор е длины k. Идея Хэмминга состоит в том, чтобы этот вектор е был в точности номером разряда, в котором произошло замещение! Остаётся только исправить данный разряд, получив точное значение сообщения b, а затем удалить из этого слова контрольные разряды – в результате получим неискажённое информационное слово a. Всё выглядит предельно просто: если 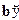 есть переданное сообщение, то
есть переданное сообщение, то 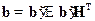 есть правильный код.
есть правильный код.
Основой для построения корректирующих кодов является теория групп – поля многочленов. — Как построить порождающие и проверочные матрицы кодов.
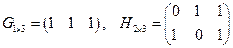 – (1, 3) код в матричном виде (код Хэмминга).
– (1, 3) код в матричном виде (код Хэмминга).
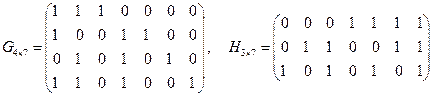 – (4, 7) код Хэмминга.
– (4, 7) код Хэмминга.
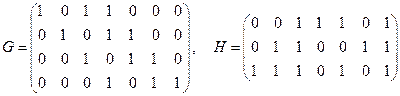 – ещё один в ленточной форме.
– ещё один в ленточной форме.
V1 = {1,3,5,7,9,…} = {ab…1} W1 = V1\{1=20} = {3,5,7,9,…} –числа, оканчивающиеся на 1.
V2 = {2,3,6,7,10,…} = {a…1b} W2 = V2\{2=21} = {3,6,7,10,…} – числа с 1 во 2–м разряде.
V3 = {4,5,6,7,12,…} = {a… 1bс} W3 = V3\{4= 22} = {5,6,7,12,…} – числа с 1 в 3–м разряде.
...
Сообщение a1,a2,…,am загружается в кодовое слово\{2i}. В разряды {2i} (их ровно k) помещается контрольная информация – номера разрядов берутся из множеств Wi поочерёдно:
c1 = a1+a2+a4+…
c2 = a1+a3+a4+…
c3 = a2+a3+a4+…
| b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | … |
| c1 | c2 | a1 | c3 | a2 | a3 | a4 | c4 | … |
Полученное сообщение b¢ проверяется суммированием по множествам индексов из Vi:
j1 = c1 + a1+a2+a4+… = b¢1 + b¢3 + …etc
j2 = c2 + a1+a3+a4+…
j3 = c3 = a2+a3+a4+…
Предложение. Если J = jl…j1 ¹ 0, то (однократный) сбой произошёл в J-ом разряде.
Дополнение.
Каким образом можно найти различные матричные (групповые) коды?
Закодируем слово а = a1a2…am многочленом а (х) = х1a1+ х2a2+… хmam. Если умножить: xn a (x), то информация будет содержаться в коэффициентах при старших степенях многочлена. Найдём остаток r (x) от деления xn a (x) на некоторый примитивный многочлен q (x). Образуем кодовый многочлен b (x) = xn a (x)– r (x) = q (x) p (x) и отправим сообщение. При получении сообщения 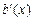 разделим его на q (x):
разделим его на q (x): 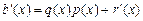 . Если
. Если 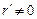 , то в канале произошёл сбой. Тогда
, то в канале произошёл сбой. Тогда 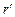 будет кодом ошибки – т.е. по его значению можно будет определить, в каком канале произошла ошибка. — Но только в том случае, если мы имеем дело с полем GF(q(x))!
будет кодом ошибки – т.е. по его значению можно будет определить, в каком канале произошла ошибка. — Но только в том случае, если мы имеем дело с полем GF(q(x))!
Пример. Пусть a =1001, m=4, k=3, n=7; q (x) = 1+x+ x3;
a (x) = 1+x3, x3 a (x) = (1+x+x3)(x+x3)+(x+x2), b (x) = x+x2+x3+x6Þ b = 011 1001 – первые 3 разряда проверочные, последние 4 – информационные. Пусть 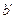 = 011 1011 Þ
= 011 1011 Þ 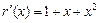 , код ошибки – 111. Можно составить таблицу код ошибки «номер разряда и исправлять сообщения.
, код ошибки – 111. Можно составить таблицу код ошибки «номер разряда и исправлять сообщения.
Другой способ: 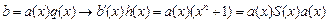
Здесь есть порождающая матрица кода, проверочная матрица кода и синдром ошибки.
 2015-06-24
2015-06-24 1443
1443








