Любой обмен информаций или передача ёё в широком смысле слова являются кодированием. Так, речь – это кодирование в звуках мыслей, текст – представление мыслей или речи в виде символов – тоже кодирование, оцифровка звука, графики и т.п. – всё это кодирование…
Вопросы кодирования играют заметную роль и в математике. Кодирование позволяет, в частности, сводить изучение одних объектов к изучению других. Два примера:
· Десятичная позиционная система кодирования, а также римская, греческая и пр.
· Метод координат – способ кодирования геометрических объектов числами.
В этих примерах средства кодирования играют вспомогательную роль и не являются предметом математического изучения. Совсем другое значение получили коды с развитием систем управления и информации. Кодирование пронизывает информационные технологии и является центральным вопросом при решении самых разных задач программирования. Среди них:
· представление данных произвольной природы – числовых массивов, текста, графики – в памяти компьютера;
· сокращение символьного текста при ограниченном количестве кодовых символов – оптимальное кодирование;
· защита информации от несанкционированного доступа – секретное кодирование;
· обнаружение и исправление ошибок при передаче и хранении информации – корректирующее кодирование;
· сжатие информации.
Редко когда перечисленные задачи выступают отдельно – на практике чаще бывает совмещение нескольких целей.
Ситуацию с достаточной полнотой может пояснить следующая схема:
| Сообщение | Кодированное сообщение | Канал связи | Принятое сообщение | Декодированное сообщение | ||
| S | К | KS=KoS | P | 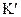 =DoKoS =DoKoS | K-1 | 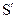 = K-1oDoKoS = K-1oDoKoS |
 |  |  |
К этой схеме можно добавить источник сообщения, помехи в канале связи, коррекцию принятого сообщения.
Все сообщения являются словами некоторых языков. Напомним в этой связи основные определения.
· Алфавитом называется конечное множество A = {a1, …, am}. Элементы алфавита называются буквами или символами.
· Словома в алфавите А называется произвольная последовательность букв.
· Вхождение буквы ak в слово а.
· Пустое слово обозначается l.
· Длина слова – количество букв в нём; обозначается как | a |, при этом | l |=0.
· Множество всех слов в алфавите А, включая пустое, обозначается А*, множество слов ненулевой длины – А+. Произвольное множество слов LÍ А* называется языком.
· На множестве А* определена операция конкатенации ^: А* ‰ А* a А*, так что ^(а1, а2) = а1а2. Алгебра (А*,^) является моноидом.
· Если слово а имеет вид а1а2, то а1 называется началом, или префиксом слова а, а а2 – суффиксом (окончанием, постфиксом) слова а.
Процедуру кодирования теперь можно сформулировать следующим образом. Пусть в некотором алфавите A = {a1, …, am} сформировано множество слов S Ì L, называемое сообщением.
Это может быть и трактат наподобие «Войны и мiра», и отдельная фраза типа «над всей Испанией безоблачное небо», слово или даже одна буква. — Всегда можно считать сообщение одним словом, если ввести в алфавит дополнительный символ – разделитель-пробел # (но не l!).
Пусть задан алфавит B = {b1, …, bn} и функция на сообщениях К: S → B *, перерабатывающая слова из алфавита A в слова из B *. Тогда функция К называется кодированием, а слова b = K(a), где а ÎS, а b ÎB* – кодами соответствующих сообщений. Обратная функция К-1 (если она существует!) называется декодированием.
Если кодовые слова представляют собой последовательности нулей и единиц, т.е. bi Î{0,1}n, то такое кодирование называется двоичным. Далее рассматривается только оно, определение «двоичное» опускается.
Выбор кодов определяется задачей. Типичная задача теории кодирования формулируется следующим образом: При заданных алфавитах А и В и множестве сообщения S найти такое кодирование F, которое обладает определёнными свойствами (т.е. оно удовлетворяет заданным ограничениям и оптимально в некотором смысле). Как правило, под оптимальностью понимаются длины кодов или сообщения в целом. Свойства, которые обычно принимаются во внимание:
· существование декодирования;
· сложность (или простота) кодирования/декодирования.
Именно здесь приходится принимать во внимание характер сообщений – связано ли оно с массивами данных, текстом или, б. м., выполнено автоматом. Далее рассматривается несколько наиболее важных задач теории кодирования.
 2015-06-24
2015-06-24 850
850








