Для любого многоугольника всегда существует прямая, проходящая во внешней для многоугольника области и не имеющая с ним общих точек.
Упражнение 45*.
Все точки пространства, не лежащие на плоскости a, разбиваются ею на две области: отрезок, соединяющий любые две точки из одной области, не содержит внутри себя ни одной точки плоскости, отрезок же соединяющий точки из разных областей содержит ровно дну точку плоскости. (Both domains again are defined with the help of an arbitrary taken point A. Consider separately cases when A, M, N do not lie on one line and, hence, define some plane b and when they do lie on the same line. Use axioms 4-7 for the first case)
Таким образом, о двух точках можно говорить, что они лежат по одну или по разные стороны от плоскости, в зависимости от того, лежат ли они в одной или в разных областях пространства, определяемых этой плоскостью. Области эти называются полупространствами.
Итак, мы доказали с вами 45 утверждений, исходя только из первых двух групп аксиом. А теперь познакомимся с третьей группой аксиом – аксиомами конгруэнтности.
Во множество всех отрезков вводится бинарное отношение, называемое отношением конгруэнтности[4]. То есть, два отрезка могут находиться или не находиться друг с другом в этом отношении. Мы заранее не предполагаем никаких свойств у этого отношения – ни симметричности, ни рефлексивности, ни транзитивности. Все свойства этого отношения определяются нижеследующими аксиомами, а другие из них уже выводятся как теоремы. Далее отношение конгруэнтности распространяется также на множества углов и треугольников.
Будем обозначать отношение конгруэнтности символом «º».
3.1. Пусть А, ВÎа, СÎb (возможно a=b). Тогда на прямой b можно найти точку D, лежащую по данную сторону от С такую, что отрезок АВ конгруэнтен отрезку CD.
Эта аксиома делает возможным откладывание отрезков, конгруэнтных данному отрезку.
3.2. если aºb и cºb, то aºb.
3.3. Пусть АВ и ВС лежат на одной прямой а и не имеют общих точек (отличных от В), отрезки DE и EF лежат на прямой b и также не имеют общих точек (отличных от Е). (Возможно при этом, что a=b). Если при этом ABºDE и BCºEF, то ACºDF.
3.4. Пусть в плоскости a дан угол Ð(h,k), а в плоскости b (не исключаем и a=b) дана прямая b и выбрана одна из двух, определяемых ею полуплоскостей b*. Пусть также на прямой b задана точка О и выбран один из двух лучей m, определяемых этой точкой. Тогда в плоскости b $! луч n| Ð(h,k)ºÐ(m,n) и все внутренние точки угла Ð(m,n) находятся в полуплоскости b*.
3.5. Если для двух треугольников А1В1С1 и А2В2С2 имеют место А1В1ºА2В2,
А1С1ºА2С2 и ÐВ1А1С1ºÐВ2А2С2, то Ð А1В1С1ºÐ А2В2С2.
Покажем, как извлекать из этих аксиом простейшие и привычные следствия, а также прокомментируем некоторые из них.
Первая аксиома позволяет откладывать отрезки и с её помощью докажем, что каждый отрезок конгруэнтен сам себе.
Отложим с помощью аксиомы 3.1. отрезок CD, конгруэнтный отрезку АВ. Дважды повторим отношение АВºCD; АВºCD и применим аксиому 3.2. Итак, отношение конгруэнтности отрезков рефлексивно. Докажем теперь, что оно также симметрично.
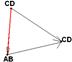 Пусть АВºCD. Тогда по только что доказанному, CDºCD и, в соответствии с 3.2., CDºАВ (см. рисунок). Теперь уже, пользуясь симметричностью и вновь аксиомой 3.2., получаем и транзитивность: аºb, bºcÞ аºb, cºbÞaºc.
Пусть АВºCD. Тогда по только что доказанному, CDºCD и, в соответствии с 3.2., CDºАВ (см. рисунок). Теперь уже, пользуясь симметричностью и вновь аксиомой 3.2., получаем и транзитивность: аºb, bºcÞ аºb, cºbÞaºc.
Итак, отношение конгруэнтности задаёт на множестве всех отрезков отношение эквивалентности. Точно так же третья аксиома позволяет откладывать углы.
Из последней аксиомы с переменой обозначений следует, что и вторая пара углов прилегающих к сторонам В1С1 и В2С2 конгруэнтна: Ð А1С1В1ºÐ А2С2В2.
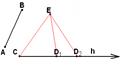 Однозначность откладывания углов в аксиоме 3.4. позволяет доказать однозначность откладывания отрезков. Допустим, что, напротив, на луче h, исходящим из точки C, имеются два отрезка, конгруэнтных отрезку АВ: СD1 и CD2. Выберем в плоскости вспомогательную точку Е и применим аксиомы 3.4. и 3.5. к треугольникам СЕD1 и CED2.
Однозначность откладывания углов в аксиоме 3.4. позволяет доказать однозначность откладывания отрезков. Допустим, что, напротив, на луче h, исходящим из точки C, имеются два отрезка, конгруэнтных отрезку АВ: СD1 и CD2. Выберем в плоскости вспомогательную точку Е и применим аксиомы 3.4. и 3.5. к треугольникам СЕD1 и CED2.
Имеем СЕºСЕ, CD1ºCD2, ÐECD1=ÐECD2. Следовательно, ÐСED1 должен был бы быть конгруэнтен углу ÐСED2.
Согласно аксиоме 3.4. луч ED1 должен был бы совпасть с лучом ED2.
Из аксиомы 3.5. выведите непосредственно простую, но важную теорему Фалеса:
 2015-06-24
2015-06-24 350
350








