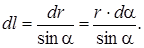Пример 7

Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t = 100 нКл/м. Определить потенциал j поля в точке пересечения диагоналей (рис. 14).

Дано: t = 1·10-10 Кл/м	Решение: Заряд, находящийся на рамке, нельзя считать точечным, он равномерно распределен по длине квадратной рамки. Поэтому для нахождения потенциала используем принцип суперпозиции
φА -?

полей. Согласно ему, потенциал поля квадратной рамки равен алгебраической сумме потенциалов полей, создаваемых

зарядом каждой стороны квадрата. Из соображений симметрии следует, что эти потенциалы равны по величине и одинаковы по знаку: j₁ = j₂ = j₃ = j₄. Тогда j = 4j_i.

Выделим на рамке малый участок dl с зарядом dQ = t·dl. Этот заряд можно рассматривать как точеч-

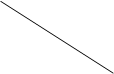
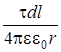r dr ный.Потенциал поля такого заряда dj = = , где r - расстояние от элемента dl до точки 0. Для интегри- рования нужно преобразовать эту формулу так, чтобы в ней была только одна переменная - угол a. Согласно чертежу Тогда

A B α1 dα dl α2 K O D C Рис. 14

dj = = .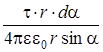

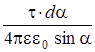Точка K делит сторону квадрата AD пополам. Тогда j _AD = 2j _AK. При

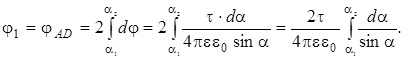вычислении потенциала φ_АК интегрирование ведется от α₁=π/4 до α₂=π/2.

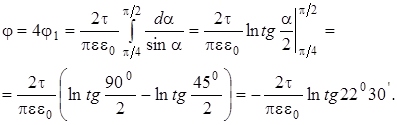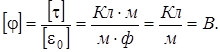Проверим единицы потенциала