Чему равна напряженность электрического поля равномерно заряженного стержня с линейной плотностью t в точке, находящейся на расстоянии R от оси стержня? Углы, образованные стержнем и прямыми, проходящими через его концы и точку A равны, соответственно a 1 и p - a 2 .
| Дано: t R a 1 p - a 2 | Решение: Расстояние от исследуемой точки поля A до оси стержня может быть любым, поэтому заряд на стержне не является точечным. Выделим на стержне элемент длины dl (рис.11). На нем располагается элементарный заряд dq = t×dl, который можно считать точечным. |
| E -? |
Напряженность поля, созданного зарядом dq в исследуемой точке, можно разложить на две составляющие, одна из которых перпендикулярна, а другая - параллельна оси стержня.
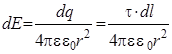 (1)
(1)
Обозначим a угол между радиусом - вектором 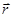 и стержнем. Радиус- вектор направлен от элемента dl к точке А. Тогда
и стержнем. Радиус- вектор направлен от элемента dl к точке А. Тогда
dE ^ = dE× sin a, dE || = dE× cos a (2)
Рис. 11 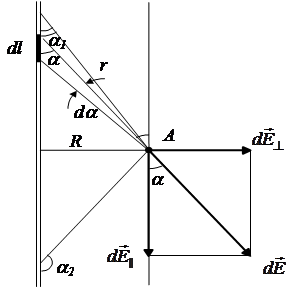 | Прежде чем интегрировать вы- ражения (2), нужно преобразо- вать выра жение (1) так, чтобы можно было интегрировать по углу a. Выразим элемент дли- ны проводника dl через da. Из рис. 11 видно что 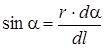 т.е. т.е. 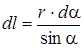 , но , но 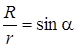 , , 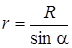 , т.е. r - величина переменная, зави- сит от a. Тогда , т.е. r - величина переменная, зави- сит от a. Тогда 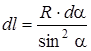 . . |
Подставив dl и r в формулу (1), получим
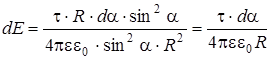 (3)
(3)
|
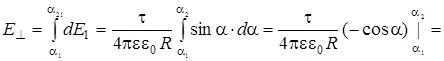
|
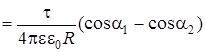 . (4)
. (4) 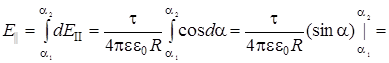
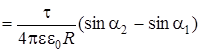 . (5)
. (5)
Модуль вектора 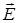 равен:
равен:
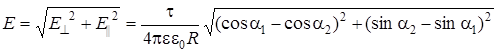 .
.
Чтобы избежать громоздких записей, преобразуем сначала подкоренное выражение:
(cos a1 - cos a2)2 + (sin a2 - sin a1)2 = cos2 a1 + cos2 a2 – 2cos a1 × cos a2 + + sin2 a2 + sin2 a1 – 2sin a2 sin a1 = (sin2 a1 + cos2 a1) + (sin2 a2 + cos2 a2) – – 2(sin a1 sin a2 + cos a1 cos a2) = 2[1 – cos(a1 - a2)] = 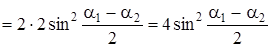 .
.
Тогда модуль напряженности:
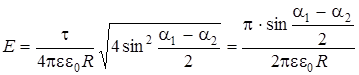 (6)
(6)
Чтобы найти направление вектора 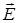 , определим угол a:
, определим угол a:
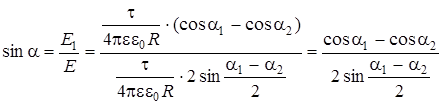
Рассмотрим частный случай: точка А находится против середины стержня. Тогда из соображений симметрии E|| = 0, E = E ^и cos a2 = - cos a1. С учетом этого формула (4) примет вид:
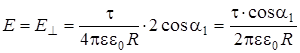 . (7)
. (7)
При этом a1 = p - a2. Покажем, что в предельных случаях поле, образованное заряженной нитью конечной длины, переходит в электрическом поле бесконечно протяженной нити и точечного заряда. Из чертежа видно, что cos a1 = cos(a - a2) = 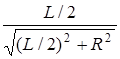 , где L - длина стержня.
, где L - длина стержня.
а) При R << L величиной R можно пренебречь и cos a 1» 1. Отсюда 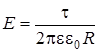 - это напряженность поля бесконечной протяженной нити. Подставим значение cos a 1 в формулу напряженности (7)
- это напряженность поля бесконечной протяженной нити. Подставим значение cos a 1 в формулу напряженности (7)

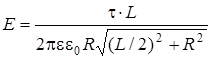
Произведение t × L = q, т.е. заряду, находящемуся на нити.
б) При R>>L величиной L /2 можно пренебречь, тогда 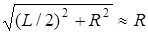 и
и 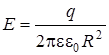 - это напряженность поля точечного заряда.
- это напряженность поля точечного заряда.
Пример 6.
В вакууме образовалось скопление зарядов в виде тонкого длинного цилиндра с объемной плотностью r =1·10-10 Кл/м3 и радиусом R = 10 см. Найти напряженность поля в точках, отстоящих от оси цилиндра на расстоянии 5 см и 15 см, а также вид зависимости Е (r).
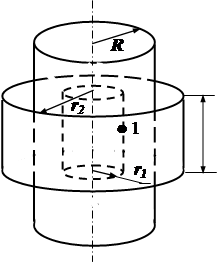
| Дано: R = 0,1 м r = 1·10-10 Кл/м3 r1 = 0,05 м r2 = 0,15 м e = 1 | Решение: Через точки 1 и 2 проведем в виде цилиндров радиусом r 1 и r 2 замкнутые поверхности (рис.12). Поток вектора напряженности, пронизывающий боковую поверхность цилиндра радиуса r 1, равен: NE(1) = E 1×2 pr 1 × l, где l - длина образующей цилиндра. (Поток через основание цилиндра равен нулю). | |||
| Е1 =? Е2 =? Е(r) =? | ||||
|
Рис. 12
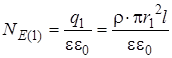 . .Отсюда: E 1×2 pr 1× l =
. .Отсюда: E 1×2 pr 1× l = 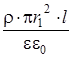
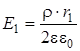 Точка 1 находится внутри цилиндра радиуса R. Поэтому для любой точки с
Точка 1 находится внутри цилиндра радиуса R. Поэтому для любой точки с 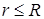 имеем:
имеем: E (r) = 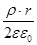 ,
,
т.е. напряженность линейно растет с увеличением расстояния.
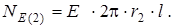 |
Поток напряженности, пронизывающий поверхность второго цилиндра, находится аналогично
По теореме Гаусса NE(2) = 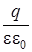 =
= 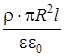 .
.
Приравнивая правые части равенств, найдем
E2 = 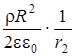 .
.
Зависимость Е (r) при r > R имеет вид
E (r) = 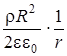
Напряженность убывает пропорционально 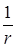 . При r = R
. При r = R
ER = 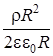 =
= 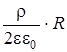
На поверхности цилиндра напряженность имеет максимальную величину.
Проверим единицы напряженности
[ E ] = 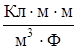 =
= 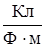 =
= 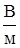 .
.
Произведем вычисления учитывая, что 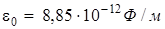
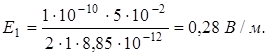
E2 = 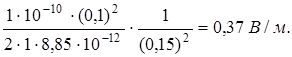
Графически зависимость Е (r) представлена на (рис.13).
| r | R | 2R | 3R | 4R | 5R | 6=R | 7R | |
| E | ER | ER/2 | ER/3 | ER/4 | ER/5 | ER/6 | ER/7 |
 |
E
ER
 2015-06-24
2015-06-24 2518
2518








