Поставленная задача для упругого (а следовательно, и любого линейно деформи-рованного) полупространства впервые была полностью решена проф. Ж.. Буссинеском
(1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости,-проф.В.Кирпичевым и проф.Н.А. Цытовичем (1923-1934).
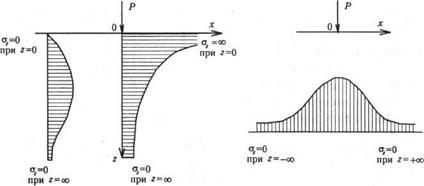
Задача определить напряжения σz, τzy,τzx, как наиболее часто используемых в расчетах.
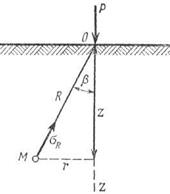
Для упрощения расчетов определяют напряжения σR в точке М с полярными координатами R и β. Окончательный результат, который полностью совпадает с решением Буссинеска, принимают как постулат, что напряжение σR пропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R2.
Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Ж.Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы.
Таким образом: 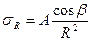 ; для перемещений:
; для перемещений: 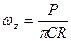
|
|
|
где: 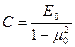 - коэф.линейно деформируемого полупространства; Е0 ,μ0 -модули общей и поперечной (аналогичный коэф. Пуассона) деформаций
- коэф.линейно деформируемого полупространства; Е0 ,μ0 -модули общей и поперечной (аналогичный коэф. Пуассона) деформаций
А - некоторый коэффициент, определяемый из условия равновесия:
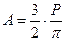
Подставляя А в формулу получим: 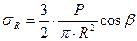 .
.
|
 2015-06-24
2015-06-24 386
386








