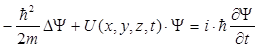 , (1)
, (1)
где ħ = h / (2π), m – масса частицы, Δ – оператор Лапласа 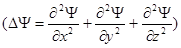 , i – мнимая единица, U (x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x, y, z, t) – искомая волновая функция частицы.
, i – мнимая единица, U (x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x, y, z, t) – искомая волновая функция частицы.
40.
В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение
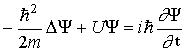 (20)
(20)
где m - масса частицы, 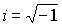 - мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа [ см. (1.10)].
- мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа [ см. (1.10)].
Решение уравнения Шредингера позволяет найти волновую функцию Y(x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства.
Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя
Y(x, y, z, t) =y(x, y, z) exp[-i(E/ 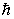 )t] (21)
)t] (21)
где E/ 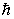 =w.
=w.
В стационарном случае уравнение Шредингера имеет вид
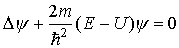 (22)
(22)
где Е, U - полная и потенциальная энергия, m - масса частицы.
Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений
41.
Из смысла пси-функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью пси-функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. На первый взгляд может показаться, что квантовая механика дает значительно менее точное и исчерпывающее описание движения частицы, чем классическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени
42.
Физический смысл волновой функции. Квадрат модуля волно-вой функции дает плотность вероятности обнаружить микрочастицу в данной точке пространства в данный момент времени
где: 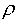 - плотность вероятности
- плотность вероятности 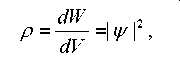 ,
,
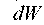 –
– 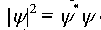 вероятность обнаружить микрочастицу в объеме
вероятность обнаружить микрочастицу в объеме 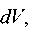
- квадрат модуля волновой функции, 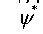 - функция комплексно-сопряженная к
- функция комплексно-сопряженная к
Свойства волновой функции. 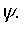
Ко нечная.
Однозначная.
Непрерывная.
Имеет непрерывные производные по координатам и времени
Удовлетворяет условию нормировки: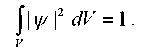
6) Справедлив принцип суперпозиции. Если 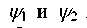 являются
являются
волновыми функциями, то любая их линейная комбинация
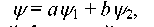
также является волновойфункцией, где 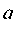 и произвольные кон-
и произвольные кон-
станты. 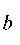
Волновая функция является решением уравнения Шредингера.
 2015-06-24
2015-06-24 365
365







