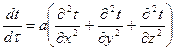 . (7)
. (7)
Уравнение (7) определяет распределение температур в любой точке тела, через которое теплота передается теплопроводностью, и называется дифференциальным уравнением теплопроводности в неподвижной среде, или уравнением Фурье.
Коэффициент пропорциональности 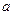 в уравнении (7) называется коэффициентом температуропроводности. Он характеризует теплоинерционные свойства тела: при прочих равных условиях быстрее нагреется или охладится то тело, которое обладает большим коэффициентом температуропроводности, и, следовательно, характеризует скорость изменения температуры в нестандартных тепловых процессах.
в уравнении (7) называется коэффициентом температуропроводности. Он характеризует теплоинерционные свойства тела: при прочих равных условиях быстрее нагреется или охладится то тело, которое обладает большим коэффициентом температуропроводности, и, следовательно, характеризует скорость изменения температуры в нестандартных тепловых процессах.
Коэффициент температуропроводности имеет следующую единицу измерения:
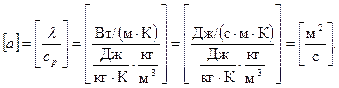
В случае установившегося процесса передачи теплоты теплопроводностью 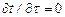 , т. е. температура не изменяется со временем. Тогда уравнение (7) примет вид
, т. е. температура не изменяется со временем. Тогда уравнение (7) примет вид
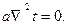 (8)
(8)
Однако величина а не может быть равна нулю и, следовательно,
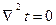 или
или 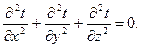 (9)
(9)
Уравнение (9) является дифференциальным уравнением теплопроводности в неподвижной среде при установившемся тепловом режиме.
Уравнения (7) и (9) описывают распределение температур в случае передачи теплоты теплопроводностью в самом общем виде и не учитывают, в частности, геометрические формы тела, через которое проводится теплота. При решении конкретных задач дифференциальные уравнения дополняются краевыми условиями, характеризующими каждую конкретную задачу.
Теплопроводность через плоскую стенку. Рассмотрим наиболее распространенный случай – теплопроводность через плоскую однослойную стенку, длина и ширина которой бесконечно велики по сравнению с ее толщиной δ (рис. 2).
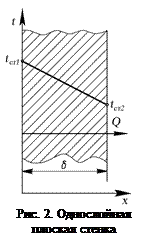 Стенка имеет во всех своих частях одинаковую толщину, температуры поверхностей t
Стенка имеет во всех своих частях одинаковую толщину, температуры поверхностей t 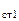 и t
и t 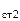 поддерживаются постоянными, т. е. являются
поддерживаются постоянными, т. е. являются  изометрическими, причем t
изометрическими, причем t 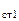 > t
> t 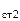 . При установившемся процессе количества теплоты, подведенного к стенке и отведенного от нее, равны между собой и не изменяются во времени.
. При установившемся процессе количества теплоты, подведенного к стенке и отведенного от нее, равны между собой и не изменяются во времени.
Температура меняется только в направлении, перпендикулярном к плоскости стенки, которое принимаем за ось x. В такой постановке температурное поле одномерное (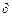 t ∕
t ∕ 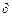 y = 0,
y = 0, 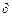 t ∕
t ∕ 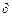 z = 0).
z = 0).
Коэффициент λ постоянен для всей стенки. При установившемся (стационарном) тепловом режиме температура в любой точке тела неизменна и не зависит от времени.
При принятых условиях в уравнении (9) первые и вторые производные от t по y и z равны нулю:
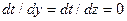 ;
; 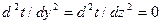 ,
,
поэтому уравнение теплопроводности можно записать в виде
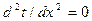 . (10)
. (10)
Интегрирование уравнения (10) приводит к функции
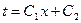 , (11)
, (11)
где C 1 и C 2 – константы интегрирования.
При постоянном коэффициенте теплопроводности λ это уравнение прямой линии. Таким образом, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.
Константы интегрирования определяют исходя из следующих граничных условий:
при x = 0 величина t = t 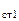 и из уравнения (11)
и из уравнения (11)

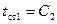 ,
,
при x = δ величина t = t 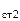 и уравнение (11) принимает вид
и уравнение (11) принимает вид
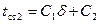 ,
,
или
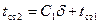 ,
,
откуда
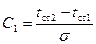 .
.
Подставив значения констант C 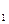 и C
и C 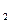 в уравнение (11), находим
в уравнение (11), находим
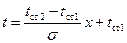 .
.
Тогда
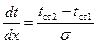 .
.
Подставив полученное выражение температурного градиента в уравнение теплопроводности (5), определим количество переданной теплоты:
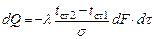 или
или 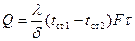 , (12)
, (12)
где λ – коэффициент теплопроводности материала стенки, Вт∕(м×К); δ – толщина стенки, м; (t 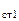 – t
– t 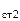 ) – разность температур поверхностей стенки, К; F – площадь поверхности стенки, м
) – разность температур поверхностей стенки, К; F – площадь поверхности стенки, м 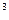 ;
; 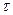 – время, с.
– время, с.
Уравнение (12) является уравнением теплопроводности плоской стенки при установившемся тепловом режиме.
 2015-06-24
2015-06-24 1696
1696
