Теплопроводность

При его изучении, прежде всего, необходимо установить понятие температурного поля и градиента температур.

Температурное поле – это совокупность значений температур в данный момент времени для всех точек рассматриваемой среды. В общем случае температура t в данной точке является функцией координат x, y, z и времени :

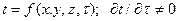. (2)

Уравнение (2) является уравнением неустановившегося (нестационарного) температурного поля, т. е. зависящего от времени. Такое поле отвечает неустановившемуся тепловому режиму теплопроводности.

В частном случае температура является функцией только системы координат и не зависит от времени:

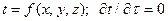. (3)

Такое температурное поле будет установившимся (стационарным).

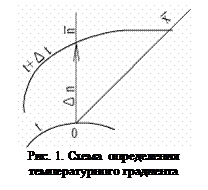Градиент температур. Если рассечь тело плоскостью и соединить точки, лежащие в этой плоскости и имеющие одинаковую температуру, то получим линии постоянных температур, называемые изотермами (рис. 1).

В пространстве геометрическое место точек с одинаковыми температурами представляет собой изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности друг с другом никогда не пересекаются. Все они или замыкаются на себя, или кончаются на границах тела. Таким образом, изучение температуры в теле имеет место только в направлениях, пересекающих изотермические поверхности (на рис. 1 это направление x). Наиболее резкое изменение температуры получается в направлении нормали n к изотермической поверхности. Предел отношения изменения температуры 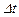к расстоянию между изотермами по нормали 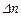называется градиентом температур и обозначается одним из следующих символов:

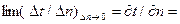grad t. (4)

Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный частной производной от температуры по этому направлению. За положительное направление градиента принимается направление возрастания температур.

Основной закон теплопроводности. Связь между потоком dQ, проходящим через элементарную площадку dF, расположенную на изотермической поверхности, за промежуток времени 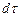, и градиентом температуры устанавливается законом Фурье (основной закон теплопроводности), согласно которому

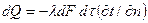, (5)

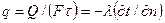, (6)

где q – плотность теплового потока или количество теплоты, передаваемое через единицу поверхности в единицу времени.

Знак минус в правой части уравнений (5) и (6) показывает, что теплота перемещается в сторону убывания температуры.

Коэффициент пропорциональности λ называется коэффициентом теплопроводности. Его единица измерения:

.

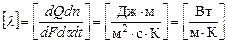Из единицы измерения очевиден физический смысл коэффициента теплопроводности: λ показывает, какое количество теплоты проходит вследствие теплопроводности в единицу времени через единицу площади поверхности теплообмена при падении температуры на один градус на единицу длины нормали к изотермической поверхности. Иными словами, коэффициент теплопроводности является физической характеристикой вещества, определяющей способность тела проводить теплоту. В общем случае λ зависит от природы вещества, его структуры, плотности, влажности, давления и температуры.

При обычных условиях наибольшее значение коэффициента теплопроводности, Вт/(м×К), имеют металлы (например, для меди λ = 384, для нержавеющей стали λ = 14…23), наименьшее – газы (например, для воздуха λ = 0,027).