При решении задач этой темы необходимо знать:
1. Типы дифференциальных уравнений первого порядка и методы их решения.
- Дифференциальные уравнения высших порядков.
- Методы решения линейных однородных дифференциальных уравнений (ЛОДУ).
- Методы решения линейных неоднородных дифференциальных уравнений (ЛНДУ).
| ДУ 1-го порядка | ||||||
| ДУ с разделяющимися переменными | Однородные ДУ | Линейные ДУ. Уравнения Бернулли | ДУ в полных дифференциалах | |||
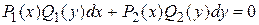 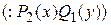 , ,
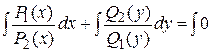 или
или
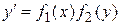 , ,
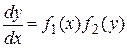 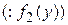
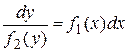 , ,
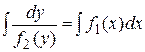 . .
| 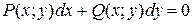 , ,
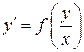 , ,
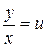 , ,
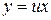 , ,
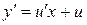 . .
| 1) 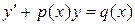 уравнение линейное относительно уравнение линейное относительно 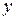 .
* метод Бернулли: .
* метод Бернулли: 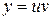 , , 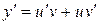 .
* метод Лагранжа: .
* метод Лагранжа: 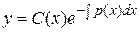 или или 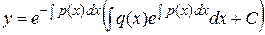 . .
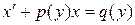 уравнение линейное относительно уравнение линейное относительно 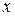 .
2) .
2) 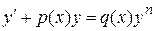 , , 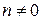 , , 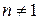 . .
| 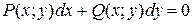 , ,
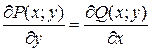 .
1 метод .
1 метод
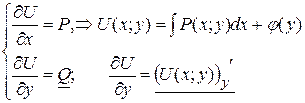 2 метод
2 метод
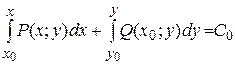
| |||
| ДУ высших порядков | ||||||
| ДУ, допускающие понижение порядка | ЛОДУ 2-го порядка | ЛНДУ 2-го порядка | Метод Лагранжа для ЛНДУ | |||
1. 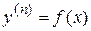 .
В частности: .
В частности: 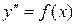 , ,
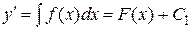 , ,
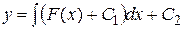 .
2. .
2. 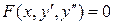 , ,
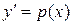 , , 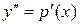 3.
3. 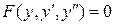 , ,
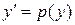 , , 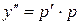
| 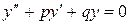 ,
характеристическое уравнение: ,
характеристическое уравнение:
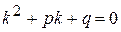 1.
1. 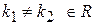 , то , то
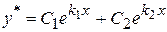 2.
2. 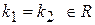 , то , то
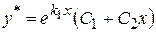 3.
3. 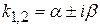 , то , то
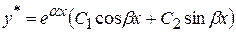
| 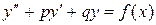 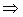 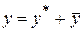 I
I 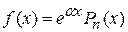 , то
Ø , то
Ø 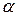 – не является корнем характеристического уравнения: – не является корнем характеристического уравнения: 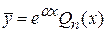 Ø
Ø 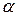 – является корнем характеристического уравнения кратности – является корнем характеристического уравнения кратности 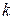 : : 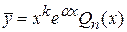 II
II 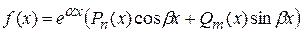 Ø
Ø 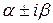 – не является корнем характе-ристического уравнения: – не является корнем характе-ристического уравнения:
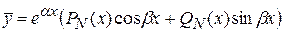 Ø
Ø 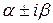 – является корнем характеристического уравнения кратности – является корнем характеристического уравнения кратности 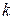 : :
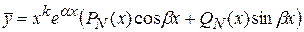
|
 , ,
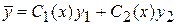 , ,
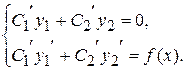
| |||
 2015-06-24
2015-06-24 227
227







