П.1.3. Функциональное уравнение логарифмической функции

Все непрерывные решения функционального уравнения

f (xy) = f(x) + f(y), (6)

справедливого для всех положительных значений x и y, имеют вид

f(x) = log _a x (a > 0, a 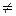1).

Докажем это. Для этого введём новую переменную ξ, изменяющуюся в промежутке (- 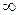; + 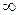), и положим

x = eξ (ведь x > 0), φ(ξ) = f(e^ξ),

откуда

ξ = ln x, f(x) = φ (ln x).

Тогда функция φ удовлетворяет функциональному уравнению (4):

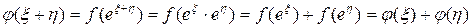
а потому

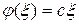и f(x) = c ln x.

Если исключить случай c = 0 (тогда f(x) 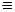0), то полученный результат может быть написан в виде

f(x) = log _a x, a = e^1/c.