Начало формы




Конец формы
Даны три множества: 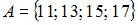 ,
, 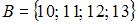 и
и 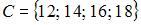 . Тогда число элементов множества
. Тогда число элементов множества 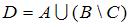 равно …
равно …
| 5 | |
Решение:
Выполним операцию в скобках, то есть определим множество 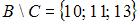 . Теперь выполним объединения
. Теперь выполним объединения 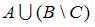 , в результате которого получится множество чисел
, в результате которого получится множество чисел 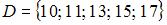 . Таким образом, множество
. Таким образом, множество 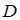 содержит пять элементов.
содержит пять элементов.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 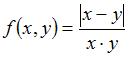 , заданная на множестве натуральных чисел …
, заданная на множестве натуральных чисел …
 | удовлетворяет всем трем аксиомам метрического пространства |
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 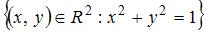 равна …
равна …
 |
Решение:
В условии дана окружность радиуса 1, то есть кривая. Ее мера равна нулю.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Биективное отображение отрезка 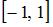 на отрезок
на отрезок 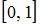 может быть задано функцией …
может быть задано функцией …
 | 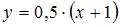 |
 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 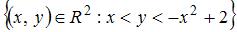 равна …
равна …
 | 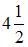 |
Решение:
Мера плоского множества 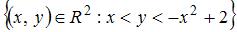 равна площади соответствующей фигуры, изображенной на рисунке:
равна площади соответствующей фигуры, изображенной на рисунке:
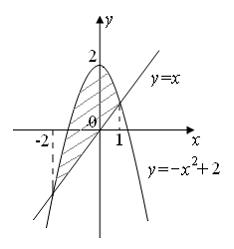
Вычислим ее с помощью определенного интеграла. 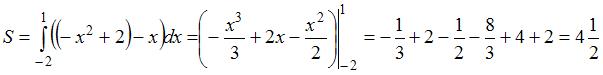 . Следовательно, мера этого множества равна
. Следовательно, мера этого множества равна 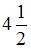 .
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны два множества: 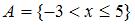 и
и 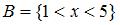 . Тогда количество целых значений
. Тогда количество целых значений 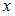 , принадлежащих объединению множеств
, принадлежащих объединению множеств 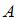 и
и 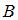 , равно …
, равно …
| 8 | |
Решение:
Объединением множеств 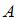 и
и 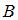 является промежуток
является промежуток 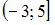 , который содержит восемь целых чисел.
, который содержит восемь целых чисел.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Прообразом множества 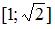 при отображении
при отображении 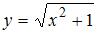 является …
является …
 | 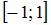 |
Решение:
Прообразом множества 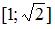 при отображении
при отображении 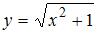 являются те точки
являются те точки 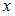 , которые при данном отображении попадают в отрезок
, которые при данном отображении попадают в отрезок 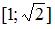 , то есть множество
, то есть множество 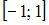 .
.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 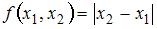 , где
, где 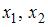 – действительные числа, …
– действительные числа, …
 | удовлетворяет всем трем аксиомам метрического пространства |
Решение:
Функция 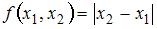 , где
, где 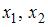 – действительные числа, удовлетворяет всем трем аксиомам метрического пространства.
– действительные числа, удовлетворяет всем трем аксиомам метрического пространства.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение, действующее из отрезка 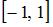 на действительную числовую ось и имеющее обратное отображение, может быть задано функцией …
на действительную числовую ось и имеющее обратное отображение, может быть задано функцией …
 |  |
Решение:
Функция, действующая из отрезка 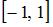 на действительную числовую ось и имеющая обратную, должна быть непрерывной и монотонной на
на действительную числовую ось и имеющая обратную, должна быть непрерывной и монотонной на 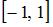 . Например, это функция
. Например, это функция 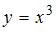 .
.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны множества: 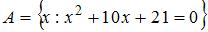 ,
, 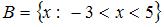 . Тогда число целых чисел, принадлежащих их объединению равно …
. Тогда число целых чисел, принадлежащих их объединению равно …
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества, изображенного на рисунке,
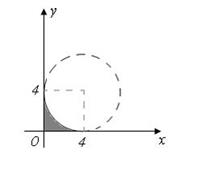
равна …
 | 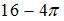 |
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 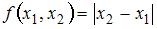 , где
, где 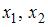 – действительные числа, …
– действительные числа, …
 | удовлетворяет всем трем аксиомам метрического пространства |
Решение:
Функция 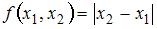 , где
, где 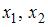 – действительные числа, удовлетворяет всем трем аксиомам метрического пространства.
– действительные числа, удовлетворяет всем трем аксиомам метрического пространства.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 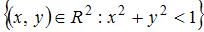 равна …
равна …
 | 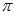 |
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение 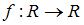 действует по правилу:
действует по правилу: 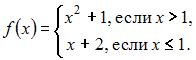 Тогда
Тогда 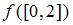 имеет вид …
имеет вид …
 | 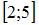 |
Решение:
Так как 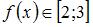 при
при 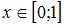 и
и 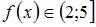 при
при 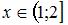 , то
, то 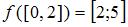 .
.
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 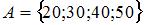 ,
, 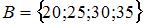 и
и 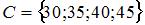 . Тогда число элементов множества
. Тогда число элементов множества 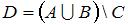 равно …
равно …
| 3 | |
Решение:
Выполним операцию в скобках, то есть определим множество 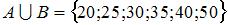 . Теперь выполним вычитание, в результате которого получится множество чисел, принадлежащих
. Теперь выполним вычитание, в результате которого получится множество чисел, принадлежащих 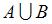 , но без чисел множества
, но без чисел множества 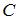 :
: 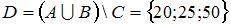 . Таким образом, множество
. Таким образом, множество 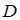 содержит три элемента.
содержит три элемента.
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 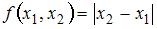 , где
, где 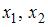 – действительные числа, …
– действительные числа, …
 | удовлетворяет всем трем аксиомам метрического пространства |
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 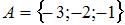 ,
, 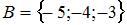 и
и 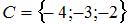 . Тогда число элементов множества
. Тогда число элементов множества 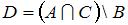 равно …
равно …
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 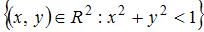 равна …
равна …
 |  |
Решение:
Мера плоского множества 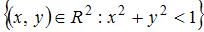 равна площади соответствующей фигуры, то есть круга с радиусом 1. Следовательно, мера этого множества равна
равна площади соответствующей фигуры, то есть круга с радиусом 1. Следовательно, мера этого множества равна 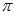 .
.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение 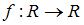 действует по правилу:
действует по правилу: 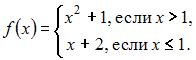 Тогда
Тогда 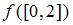 имеет вид …
имеет вид …
 | 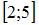 |
Решение:
Так как 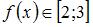 при
при 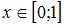 и
и 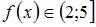 при
при 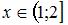 , то
, то 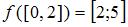 .
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 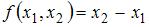 , где
, где 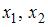 – действительные числа, …
– действительные числа, …
 | не удовлетворяет аксиоме симметрии |
Решение:
Функция 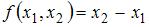 , где
, где 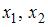 – действительные числа, не удовлетворяет аксиоме симметрии, так как
– действительные числа, не удовлетворяет аксиоме симметрии, так как 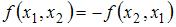 .
.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 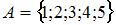 ,
, 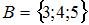 и
и 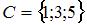 . Тогда число элементов множества
. Тогда число элементов множества 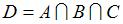 равно …
равно …
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Не может служить метрикой пространства 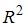 функция …
функция …
 | 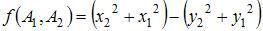 |
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение 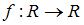 действует по правилу:
действует по правилу: 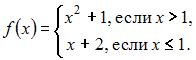 Тогда
Тогда 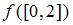 имеет вид …
имеет вид …
 | 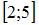 |
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 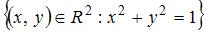 равна …
равна …
 |
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Плоская мера отрезка [0; 1], лежащего на оси 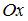 в плоскости
в плоскости  равна …
равна …
 |
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны два множества: 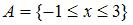 и
и 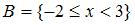 . Тогда количество целых значений
. Тогда количество целых значений 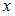 , принадлежащих пересечению множеств
, принадлежащих пересечению множеств 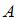 и
и 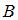 , равно …
, равно …
| 4 | |
Решение:
Пересечением множеств 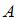 и
и 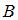 является промежуток [-1; 3), который содержит четыре целых числа.
является промежуток [-1; 3), который содержит четыре целых числа.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Обратимым на  является отображение …
является отображение …
 | 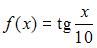 |
Решение:
Отображение 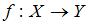 называется обратимым, если существует отображение
называется обратимым, если существует отображение  такое, что
такое, что 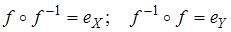 , где
, где 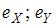 – тождественные отображения на множествах
– тождественные отображения на множествах 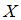 и
и 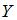 соответственно.
соответственно.
По критерию обратимости: отображение 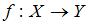 будет обратимым, если оно инъективно и сюръективно.
будет обратимым, если оно инъективно и сюръективно.
Отображение 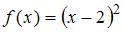 на отрезке
на отрезке 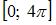 не инъективно, например, для точек
не инъективно, например, для точек 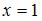 и
и 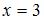 образы совпадают:
образы совпадают: 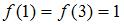 .
.
Отображения 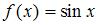 и
и 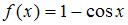 также не инъективны, например, для точек
также не инъективны, например, для точек 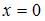 и
и 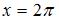 в обоих случаях
в обоих случаях 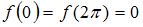 . Отображение
. Отображение 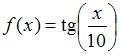 инъективно (для
инъективно (для 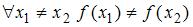 ) и сюръективно (отрезок
) и сюръективно (отрезок 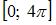 переходит в отрезок
переходит в отрезок  ); обратным для него будет отображение
); обратным для него будет отображение 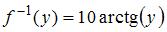 .
.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 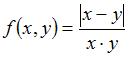 , заданная на множестве натуральных чисел …
, заданная на множестве натуральных чисел …
 | удовлетворяет всем трем аксиомам метрического пространства |
Решение:
Проверим выполнение аксиом метрического пространства:
А) 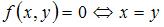 ,
,
Б) 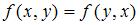 ,
,
В) 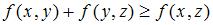 .
.
Пусть 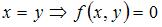 .
.
Обратно 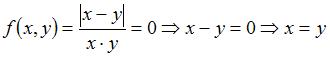 .
.
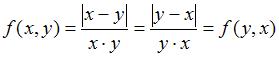 .
.
Составим неравенство треугольника для 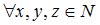
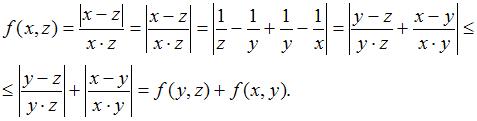
Таким образом, заданная функция удовлетворяет всем аксиомам метрики на множестве натуральных чисел.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 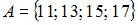 ,
, 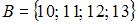 и
и 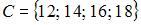 . Тогда число элементов множества
. Тогда число элементов множества 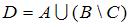 равно …
равно …
| 5 | |
Решение:
Выполним операцию в скобках, то есть определим множество 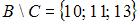 . Теперь выполним объединения
. Теперь выполним объединения 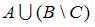 , в результате которого получится множество чисел
, в результате которого получится множество чисел 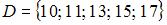 . Таким образом, множество
. Таким образом, множество 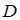 содержит пять элементов.
содержит пять элементов.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Расстояние между точками 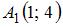 и
и 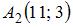 в метрике
в метрике 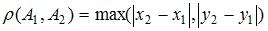 , где
, где 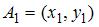 и
и 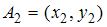 , равно …
, равно …
 |
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Плоская мера отрезка [0; 1], лежащего на оси 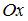 в плоскости
в плоскости 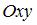 равна …
равна …
 |
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Обратимым на 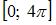 является отображение …
является отображение …
 | 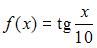 |
Решение:
Отображение 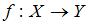 называется обратимым, если существует отображение
называется обратимым, если существует отображение  такое, что
такое, что 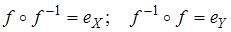 , где
, где 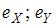 – тождественные отображения на множествах
– тождественные отображения на множествах 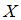 и
и 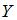 соответственно.
соответственно.
По критерию обратимости: отображение 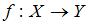 будет обратимым, если оно инъективно и сюръективно.
будет обратимым, если оно инъективно и сюръективно.
Отображение 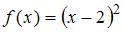 на отрезке
на отрезке 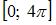 не инъективно, например, для точек
не инъективно, например, для точек 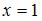 и
и 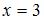 образы совпадают:
образы совпадают: 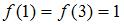 .
.
Отображения 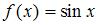 и
и 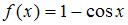 также не инъективны, например, для точек
также не инъективны, например, для точек 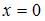 и
и 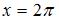 в обоих случаях
в обоих случаях 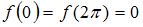 . Отображение
. Отображение 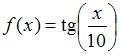 инъективно (для
инъективно (для 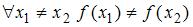 ) и сюръективно (отрезок
) и сюръективно (отрезок 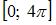 переходит в отрезок
переходит в отрезок  ); обратным для него будет отображение
); обратным для него будет отображение 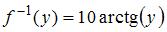 .
.
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 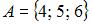 ,
, 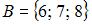 и
и 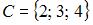 . Тогда число элементов множества
. Тогда число элементов множества 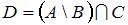 равно …
равно …
| 1 | |
Решение:
Определим множество 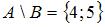 и выполним операцию пересечения
и выполним операцию пересечения 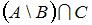 . В результате получится множество
. В результате получится множество 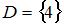 , состоящее из одного элемента.
, состоящее из одного элемента.
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Плоская мера множества 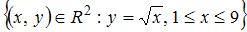 равна …
равна …
 |
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Расстояние между точками 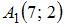 и
и 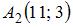 в метрике
в метрике 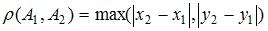 , где
, где 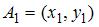 и
и 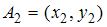 , равно …
, равно …
 |
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Прообразом множества 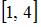 при отображении
при отображении 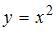 является …
является …
 | 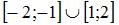 |
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Обратимым на 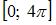 является отображение …
является отображение …
 | 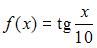 |
 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества 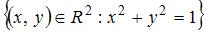 равна …
равна …
 |
 ЗАДАНИЕ N 33 сообщить об ошибке
ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 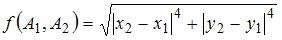 , где
, где 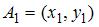 и
и 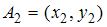 , …
, …
 | не удовлетворяет аксиоме треугольника |
Решение:
Функция 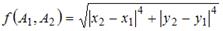 , где
, где 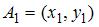 и
и 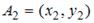 , не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
, не удовлетворяет аксиоме треугольника, например, для точек (-1, -1), (0, 0) и (1, 1).
 ЗАДАНИЕ N 34 сообщить об ошибке
ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 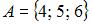 ,
, 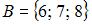 и
и 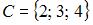 . Тогда число элементов множества
. Тогда число элементов множества 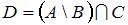 равно …
равно …
 ЗАДАНИЕ N 41 сообщить об ошибке
ЗАДАНИЕ N 41 сообщить об ошибке
Тема: Метрические пространства
Начало формы




Конец формы
Функция 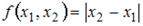 , где
, где 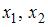 – действительные числа, …
– действительные числа, …
 | удовлетворяет всем трем аксиомам метрического пространства |
 ЗАДАНИЕ N 42 сообщить об ошибке
ЗАДАНИЕ N 42 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Мера плоского множества, изображенного на рисунке,
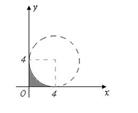
равна …
 | 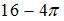 |
 ЗАДАНИЕ N 43 сообщить об ошибке
ЗАДАНИЕ N 43 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны три множества: 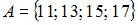 ,
, 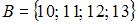 и
и 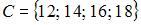 . Тогда число элементов множества
. Тогда число элементов множества 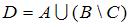 равно …
равно …
| 5 | |
Решение:
Выполним операцию в скобках, то есть определим множество 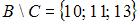 . Теперь выполним объединения
. Теперь выполним объединения 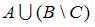 , в результате которого получится множество чисел
, в результате которого получится множество чисел 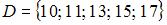 . Таким образом, множество
. Таким образом, множество 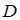 содержит пять элементов.
содержит пять элементов.
 ЗАДАНИЕ N 44 сообщить об ошибке
ЗАДАНИЕ N 44 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение 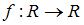 действует по правилу:
действует по правилу: 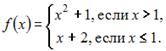 Тогда
Тогда 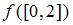 имеет вид …
имеет вид …
 | 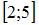 |
Решение:
Так как 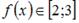 при
при 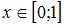 и
и 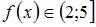 при
при 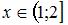 , то
, то 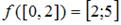 .
.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Отображение множеств
Начало формы




Конец формы
Отображение 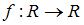 действует по правилу:
действует по правилу: 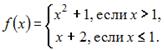 Тогда
Тогда 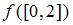 имеет вид …
имеет вид …
 | 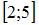 |
Решение:
Так как 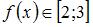 при
при 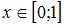 и
и 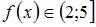 при
при 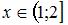 , то
, то 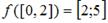 .
.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Элементы теории множеств
Начало формы




Конец формы
Даны два множества: 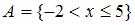 и
и 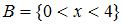 . Тогда количество целых значений
. Тогда количество целых значений 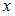 , принадлежащих разности множеств
, принадлежащих разности множеств 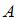 \
\ 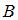 , равно …
, равно …
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Мера плоского множества
Начало формы




Конец формы
Плоская мера отрезка [0; 1], лежащего на оси 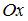 в плоскости
в плоскости 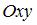 равна …
равна …
|
|

 2015-06-24
2015-06-24 2080
2080







