Отображения множеств

Большую роль в математике имеет установление связей между двумя множествам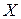и и 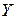, связанное с рассмотрением пар объектов, образованных из элементов первого множества и соответствующих элементов второго множества. Особое значение при этом имеет отображение множеств.

Пусть 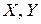- произвольные множества. Отображением множества X в множество Y называется всякое правило f, по которому каждому элементу множества 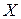сопоставляется вполне определенный (единственный) элемент множества .

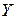Тот факт, что f есть отображение 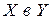, кратко записывают в виде: .

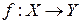Применяют также обозначение 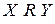. Чаще отображения обозначают буквами f, q, F.

Итак, чтобы задать отображение 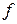множества Х в множество 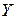, надо каждому элементу 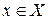поставить в соответствие один и только один элемент .

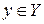Если при этом элементу х из Х сопоставлен элемент 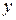из Y, то 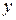называют образом элемента х, а х – прообразом элемента 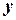при отображении 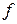, что записывается в виде .

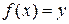Из определения отображения 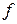следует, что у каждого элемента 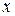из Х образ единственный, однако для элемента 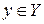прообразов может быть много, а может и вообще не быть. Множество всех прообразов элемента 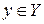называется его полным прообразом и обозначается через 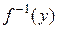. Таким образом, .

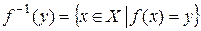Естественным путем определяются образ 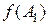подмножества 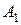из А и прообраз 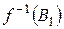подмножества 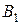из В при отображении :

, .

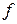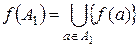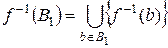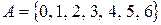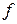Например, пусть и - отображение А в А, сопоставляющее каждому элементу а из А остаток от деления а на число 4. Тогда имеем:

;

;

.

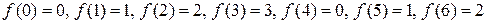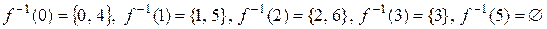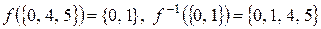В зависимости от свойств, образов и прообразов различают отображения сюръективные, инъективные и биективные.

Отображение 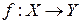называется сюръективным, если 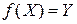, т.е. каждый элемент из 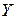отображается хотя бы один элемент из Х, или 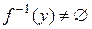при любом .

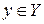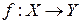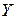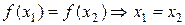Отображение называется инъективным, если разные элементы множества Х отображаются в разные элементы множества т.е. , или 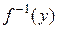является либо пустым, либо одноэлементным множеством при любом 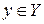. Инъективные отображения называются также вложениями.

Отображение 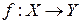называется биективным, или взаимно однозначным отображением 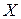на 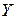, если оно сюръективно и инъективно, т.е. если 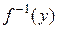есть одноэлементное множество при любом 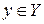. В этом случае можно определить отображения 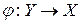, положив для любого 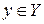: 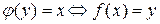. Оно называется обратным к 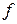и обозначается в виде .

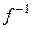Изобразим для наглядности виды отображений.

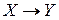
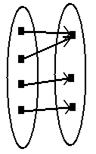
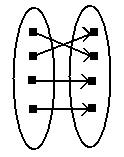
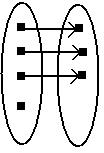
Сюръективное Инъективное Биективное

Рисунок 12

Отображение множества А в себя называется преобразованием множества А. Биективное преобразование множества А называется подстановкой множества А.

Примером подстановки множества целых чисел может служить отображение 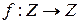, определенное равенством .

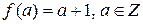Заметим еще, что отображение 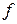множества А в В называют также функцией, заданной на множестве А со значениями в множестве В. При этом элемент 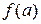называют значением функции 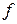точке а. Само множество А называют областью определения функции 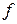, а множество 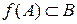- областью значений функции .

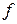Функцию 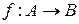зачастую трактуют как переменную величину 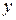, принимающую значения из В и так зависящую от переменной величины х, принимающей значения из А, что каждому значению а переменной величины х соответствует вполне определенное значение 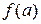величины 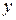. При этом пишут 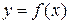и вместо «функция 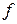» говорят «функция ».

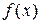Рассмотрим различные отображения и определим их виды.

1) Пусть Х – множество окружностей на плоскости. Сопоставляя каждой окружности ее центр, получим отображение Х на 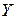. Это отображение 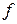не является инъективным, поскольку одна и та же точка может быть центром бесконечного множества окружностей. Но оно сюръективно, так как любая точка – центр некоторой окружности. Поэтому обратное соответствие 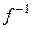всюду определено, сюръективно, но не функционально.

2) Соответствие 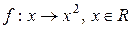является числовой функцией заданной на всем множестве 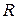действительных чисел. Множеством значений этой функции является совокупность 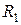неотрицательных чисел. Так как 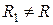, то функция 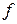не сюръективна. Она и не инъективна, так как 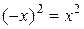. Поэтому она не имеет обратной функции.

3) Отображение 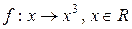сюръективно и инъективно: для любого 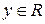есть одно и только одно число 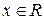такое, что 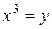. Этим числом является .

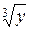4) Отображение 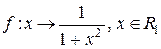( 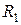- множество неотрицательных чисел) множества 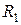в себя всюду определено, инъективно, но не сюръективно. Действительно, для дроби 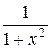, выполнено .

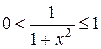Поэтому множеством значений этой функции является промежуток 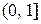. Обратная функция определена на этом промежутке и принимает неотрицательные значения.

5) Отображение 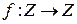, определенное правилом 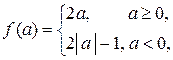является инъективным отображением. Оно не является биективным, поскольку 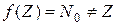. Однако, если таким же образом определить отображение 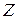в 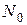, то получим биективное отображение.

В теории и на практике часто приходится осуществлять последовательно различные отображения множеств. В связи с этим дадим определение:

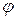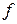Композицией отображений и , где 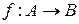, 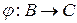называется отображение 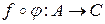, определенное условием:

. (*)

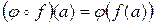Композиция 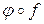отображений 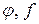называется также произведением отображений 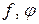и обозначается в виде 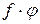, или 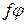. Таким образом : .

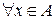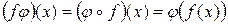Отметим некоторые свойства композиций отображений.

1. Если ,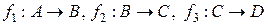

то . (**)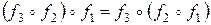

Для доказательства найдем образ элемента а из А при действии отображений, записанных в левой и правой частях равенства (**). Из (*) имеем:

,

.

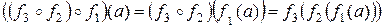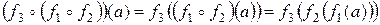Отсюда и следует (**).

2. Если отображение 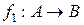, 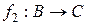сюръективны, инъективны и биективны, то соответственно таким же будет и отображение .

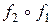Предлагаем читателю доказать это утверждение самостоятельно.

Заметим, что в общем случае из биективности 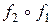не следует биективность 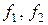; из сюръективности 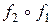следует сюръективность лишь 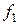, а из инъективности 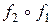следует инъективность лишь .

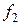3. Есл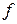и и 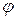- преобразования множества А, то их композиция 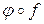также является преобразованием множества А.