Предел произведения функций

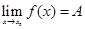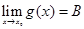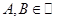Теорема: Если , а (), то .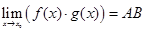

Примечание: 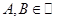- важное условие! Потому что, если один из пределов - бесконечность, то теорема не работает.

Доказательство:

1. Сначала введём некоторые определения и докажем лемму.

Определение: Функция называется ограниченной сверху (снизу) в точке x₀, если 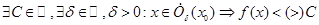(читается: <...>, если существует константа C и число d > 0 такие, что для любого x, принадлежащего выколотой d-окрестности точки x₀ выполнено f(x) меньше (или больше - для ограниченности снизу) C).

Определение: Функция называется ограниченной (ограниченной по модулю) в точке x₀, если .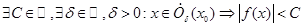

Примечание: ограниченность функции рассматривается всегда в какой-то точке.

Лемма 1. Если функция ограничена сверху и снизу (в точке x₀), то она ограничена по модулю.

Доказательство:

Пусть f(x) ограничено сверху константой C₁ в d₁-окрестности, а снизу константой C₂ в d₂-окрестности.

Тогда в окрестности :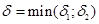

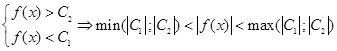[1]. Значит, для C = max (|C₁|; |C₂|) верна ограниченность.

Ч. т. д.

Лемма 2. Если функция имеет предел в точке, то она ограничена по модулю.

Доказательство:

По определению предела: 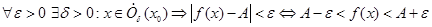. Из этого видно, что для любого 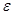(можно взять, например 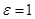) f(x) ограничена сверху и снизу. Значит, она ограничена по модулю.

Ч. т. д.

2. Докажем нашу теорему. Теперь это просто:

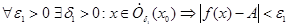
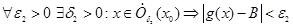
Пользуясь леммой 2 будем считать, что f(x) ограничено константой C.

Пусть 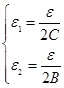( 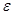дан исходно для нахождения предела произведения, откуда такие числа будет ясно позже), 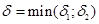для своих 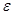. Тогда рассмотрим (вопрос обозначает, что это нужно доказать):

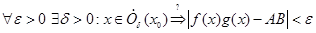. Преобразуем:

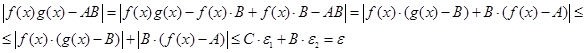
Ч.т.д.

[1] Это следствие легко проверить: 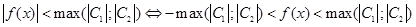. Далее нужно аккуратно сравнить 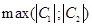с нулём и/или константами и использовать исходные неравенства. Напишу, если будет непонятно.