Экстремумы функции нескольких переменных

Определение.

Пусть 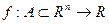и точка 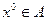. Точка 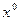называется точкой локального минимума (максимума), если 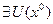, такая что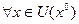 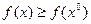для точки минимума и 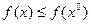для точки максимума.

Теорема (необходимое условие существования локального экстремума).

Пусть 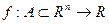и точка 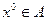. Пусть существуют частные производные 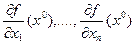. Если 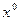– точка локального экстремума, то 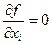для i=1, 2, …,n.

Доказательство.

Рассмотрим функцию 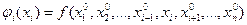. Если 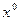– точка локального экстремума для 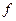, то – то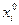чка локального экстремума для 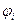. Так как существует производная 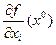, то существует производная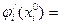 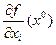. По теореме Ферма о необходимом условии существования локального экстремума (для функции одной переменной): 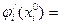0, следовательно 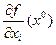=0. Это верно для всех .

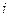Теорема (достаточное условие существования локального экстремума). Пусть 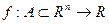и точка 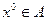и 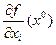=0 для всех i=1,2, …,n.Пусть f – дважды дифференцируема в точке 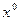, то - то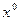чка локального максимума, если 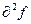отрицательно определен, 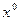- точка локального минимума, если 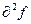положительно определен. Если 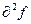не является ни положительно, ни отрицательно определенным, то экстремума нет.

Доказательство.

Рассмотрим разложение по формуле Тейлора второго порядка с остаточным членом в форме Пеано.

,

.

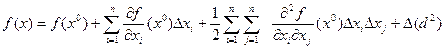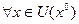
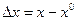Так как 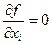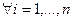следует, что =

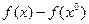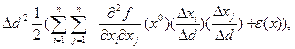
где .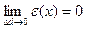

Пусть 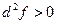, то есть второй дифференциал положительно определен.

Тогда 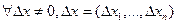следует, что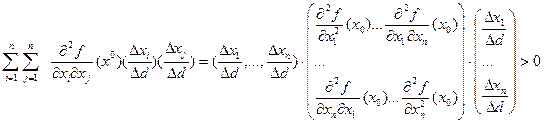

.

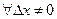Обозначим .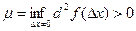

Так как 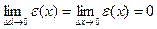, то 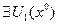, такая что 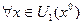справедливо следующее: 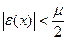, тогда знак 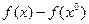определяется первым слагаемым правой части следовательно:

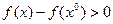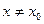
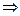
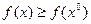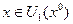
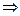
при при 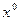- точка локального минимума.

Аналогично, если 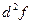отрицательно определен, то .

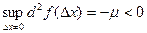Выберем окрестность 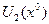такую что 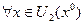: 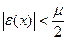, следовательно:

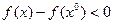
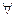
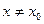
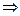
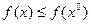
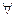
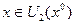
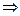
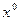- точка локального максимума.

Пусть 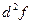не является ни положительным, ни отрицательно определенным. Значит найдутся векторы в 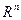U и V, такие что 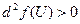и .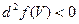

Заметим, что .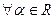

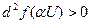В самом деле (знак сохраняется так как квадратичная форма) ().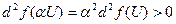

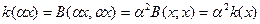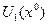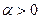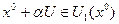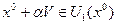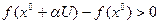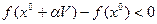
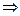
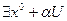Пусть - произвольная окрестность, можно взять , такой что и при этом и и 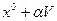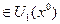, так что

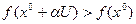и

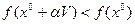
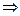локального экстремума нет.

Замечание: при решении задач на определение достаточных условий экстремума удобно применять критерий Сильвестра.

Контрпример: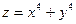

(0;0) – точка локального минимума.

.

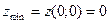Однако 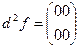- не является.