Теорема: Пусть 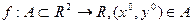 и f имеет в некоторой окрестности
и f имеет в некоторой окрестности 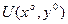 все частные производные до (n+1)-го порядка включительно. Тогда
все частные производные до (n+1)-го порядка включительно. Тогда 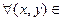
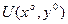 имеет место формула Тейлора с остаточным членом в форме Лагранжа:
имеет место формула Тейлора с остаточным членом в форме Лагранжа:
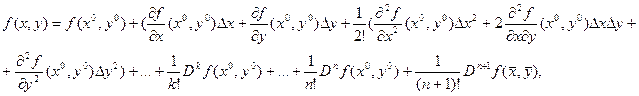 где
где 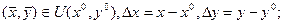 .
.
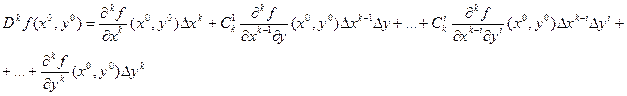 Доказательство.
Доказательство.
Выберем 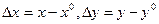 , такие что
, такие что 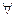
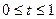
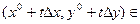
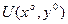 и рассмотрим функцию
и рассмотрим функцию 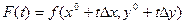 при фиксированных
при фиксированных 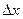 и
и 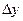 .
.
Вычислим 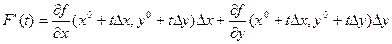 ,
,
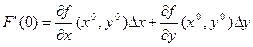 ;
;

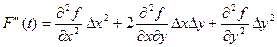 ,
,
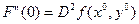 ;
;
…
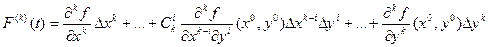 ,
,
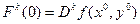 .
.
Продолжим F(t) на (- 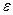 ;1] при некотором
;1] при некотором 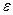 >0. Применим к F(t) формулу Тейлора в т. 0 с остаточным членом в форме Лагранжа. Получаем:
>0. Применим к F(t) формулу Тейлора в т. 0 с остаточным членом в форме Лагранжа. Получаем:
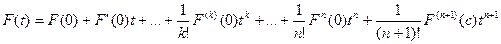 ,
,
где c – некоторое число и 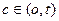 .
.
Подставим вместо t единицу и заметим, что F(1)= 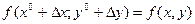 .
.
Тогда получаем:
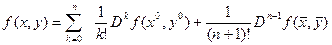 ,
,
где 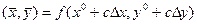

Пример.
Найти разложение 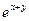 в т (0;0) по формуле Тейлора 3-го порядка.
в т (0;0) по формуле Тейлора 3-го порядка.
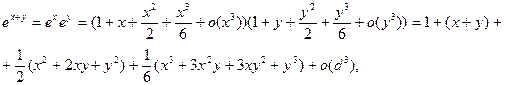
где 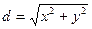 .
.
Замечание: если функция z=f(x,y) имеет все частные производные n-ого порядка в точке (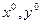 ), то имеет место формула Тейлора с остаточным членом в форме Пеано:
), то имеет место формула Тейлора с остаточным членом в форме Пеано:
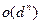 , где
, где 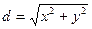 .
.
 2015-06-26
2015-06-26 207
207







