2015-06-26
1631
Определение. Отображением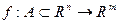 
называется однозначное соответствие точке из 
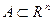точки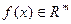 
.
Часто рассматриваются непрерывные отображения.
Определение. Отображение 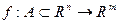называется непрерывным в точке 
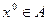, если 
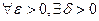такое, что 
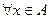и удовлетворяющего условию 
.
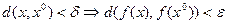Определение. Проекцией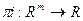 
называется функция, которая ставит в соответствие каждой точке 
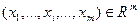точку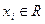 
.
Определение. Отображение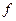 
: 
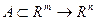задается n функциями от m переменных:
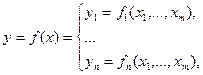
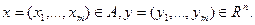
Функции f называются координатными функциями отображения f, j=1, 2, …, n.
Замечание. Отображение 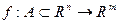может быть рассмотрено как вектор из координатных функций 
.
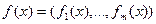Определение. Отображение 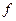называется дифференцируемым в точке 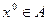, если существует линейное отображение 
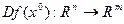такое, что 
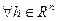и 
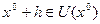где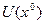 
- некоторая окрестность имеет место формула 
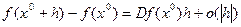, где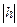 
- длина вектора 
.
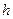Теорема. Пусть 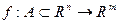и 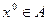. 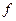дифференцируема в точке 
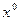тогда и только тогда, когда для любого 
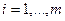координатная функция 
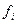дифференцируема в точке 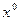. Кроме того
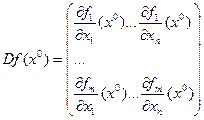- матрица Якоби (Якобиан).
Доказательство (необходимость). Пусть 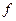дифференцируема в точке 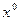, тогда для любого 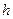такого, что точка 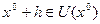имеет место разложение .
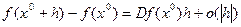Пусть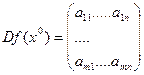 
, тогда 
.
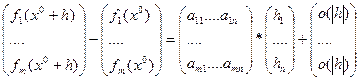Рассмотрев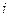 
координату вектора, получаем 
.
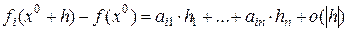Это означает, что 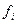дифференцируема в точке 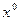и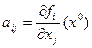 
.
Достаточность. Пусть 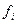дифференцируема в точке 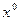, для 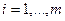. Тогда 
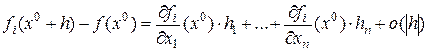. Составляем вектор из 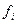и получаем дифференцируемость отображения.
