Векторным произведением вектора  на вектор
на вектор 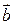 называется третий вектор, обозначаемый символом
называется третий вектор, обозначаемый символом 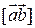 и удовлетворяющий условиям:
и удовлетворяющий условиям:
1) 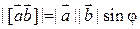 , где
, где 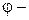 угол между векторами
угол между векторами  и
и 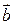 ;
;
2) вектор 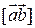 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и 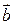 ;
;
3) тройка векторов  ,
, 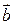 ,
, 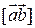 имеет ту же ориентацию, что и тройка единичных координатных векторов
имеет ту же ориентацию, что и тройка единичных координатных векторов 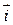 ,
, 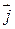 ,
, 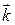 (рис.1.16).
(рис.1.16).
В дальнейшем будем предполагать, что тройка 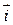 ,
, 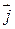 ,
, 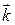 является правой.
является правой.
Модуль векторного произведения 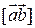 равен площади
равен площади 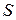 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и 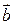 :
: 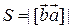 .
.
Векторное произведение можно представить в виде 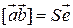 , где
, где 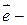 орт векторного произведения
орт векторного произведения 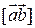 .
.
Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы  и
и 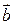 коллинеарны:
коллинеарны: 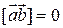 , если
, если 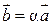 .
.
С в о й с т в а в е к т о р н о г о п р о и з в е д е н и я:
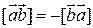 ;
;
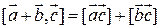 ;
;
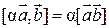 .
.
Если векторы  и
и 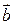 заданы своими прямоугольными координатами
заданы своими прямоугольными координатами
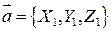 ;
; 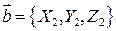 ,
,
то 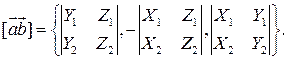
Пример 1. Дан треугольник с вершинами 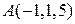 ;
; 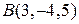 ,
, 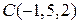 . Найти длину высоты, опущенной из вершины
. Найти длину высоты, опущенной из вершины 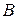 на сторону
на сторону 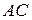 .
.
Чтобы решить задачу, достаточно вычислить площадь треугольника 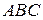 и длину стороны
и длину стороны 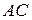 . Площадь треугольника
. Площадь треугольника 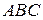 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 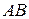 и
и 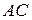 . Находим координаты этих векторов и координаты их векторного произведения:
. Находим координаты этих векторов и координаты их векторного произведения:
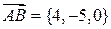 ;
; 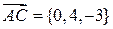 ;
; 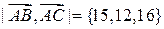 .
.
Находим площадь параллелограмма
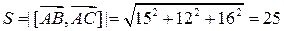 .
.
Так как 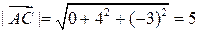 и
и 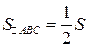 ,
, 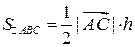 ,
,
то 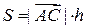 , откуда
, откуда 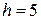 .
.
 2015-06-26
2015-06-26 464
464







