Векторы и линейные операции над ним

Элементы векторной алгебры

Вектором называется направленный отрезок. Если начало вектора находится в точке 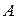, конец – в точке 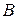, то вектор обозначается символом 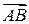или 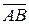. Вектор иногда обозначается одной строчной буквой жирного шрифта 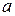, 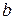и т. д. или такой же буквой светлого шрифта с черточкой наверху: , 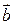и т. д.

Модулем вектора называется его длина. Он обознается через 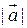или просто через .

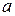Нулевым вектором называется вектор, начало и конец которого совпадают. Нуль-вектор обозначается символом 0.

Единичным вектором называется вектор, длина которого равна единице.

Векторы, лежащие на параллельных прямых (или на одной и той же прямой), называются коллинеарными.

Коллинеарные векторы, имеющие одинаковые направления и равные длины, называются равными.

Векторы противоположно направленные и имеющие равные длины называются противоположными.

Линейными операциями над векторами называются сложение, вычитание и умножение вектора на число.

Суммой двух векторов и 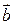называется третий вектор 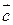, начало которого совпадает с началом вектора , конец – с концом вектора 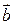, при условии, что вектор 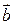отложен из конца вектора .

Сумма двух векторов обладает свойством коммутативности

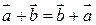
и свойством ассоциативности

.

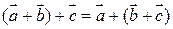Суммой 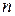векторов 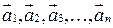называется вектор, начало которого совпадает с началом вектора , конец – с концом вектора 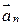, при условии, что точка приложения каждого последующего вектора совпадает с концом предыдущего.

Разностью 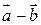двух векторов и 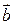называется такой вектор 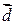, который при сложении с вектором 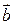дает вектор :

, .

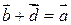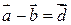Произведением вектора на число 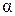называется новый вектор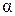 , длина которого равна 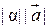, а направление совпадает с направлением вектора при 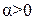и противоположно ему при .

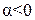Необходимое и достаточное условие коллинеарности векторов и 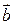выражается равенством .

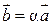Линейной комбинацией векторов 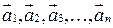называется вектор

,

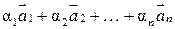где 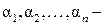действительные числа.

Векторы 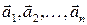называются линейно зависимыми, если существуют числа 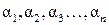, не равные одновременно нулю, такие, что

.

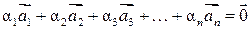В противном случае векторы называются линейно независимыми.

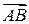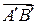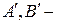Проекцией вектора на ось Ои называется величина вектора , где проекции точек 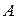и 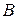на эту ось.

Если 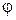- угол между вектором и осью Ои, то проекция вектора на ось Ои равна произведению длины этого вектора на косинус угла :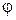

.

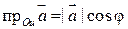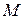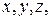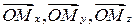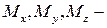Прямоугольными декартовыми координатами точки в пространстве называются числа равные величинам векторов , где проекции этой точки на взаимно перпендикулярные координатные оси: ось Ох (абсцисс), ось Оу (ординат), ось Оz (аппликат), т. е.

.

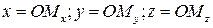Координатами вектора относительно прямоугольной системы координат 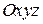называются проекции 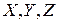вектора на оси координат:

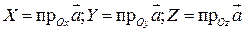
Запись 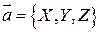или 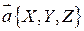означает, что вектор имеет координаты .

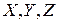Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат. Координаты произведения вектора на число равны произведениям соответствующих координат вектора на это число.

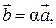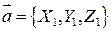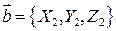Если где ; , то 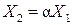; ; 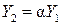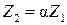. Эти равенства выражают необходимое и достаточное условие коллинеарности векторов и .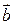

Радиус-вектором точки 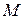называется вектор 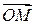, начало которого совпадает с началом координат, а конец – с точкой .

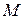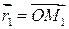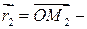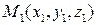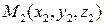Если и радиус-векторы точек и , то вектор 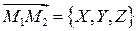выражается формулой 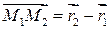, т. е. ; ; .

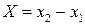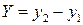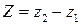Радиус-вектор точки 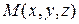, делящей направленный отрезок 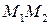, где 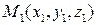; 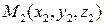, в данном отношении 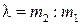, выражается формуло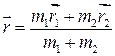й или 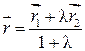, в которой , .

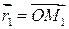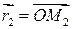Координаты точки 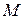находятся по формулам

; ; .

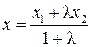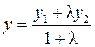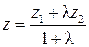Если 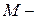середина отрезка 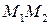, то ; ; .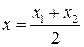

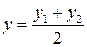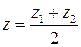Если 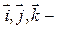единичные векторы (орты) координатных осей 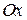, , 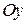, 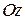то вектор 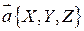можно представить в виде 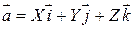. Векторы 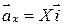; ; 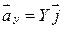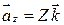называются составляющими или к омпонентами вектора.

Длина вектора вычисляется по формуле .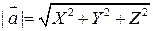

Направляющими косинусами вектора называются косинусы углов 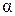, , 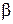, 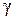образованных этим вектором с осями координат , , .

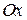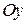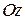Для направляющих косинусов вектора выполняется равенство

.

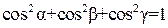Координаты вектора через направляющие косинусы выражаются формулами: 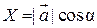; ; 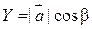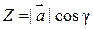. Координаты единичного вектора равны его направляющим косинусам.