Теорема о верхних и нижних границах подмножества

Если B Í A то, inf B 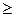inf A; sup B 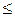sup A.

Доказательство.

Пусть 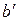- элемент множества B, имеющей наименьшее значение, т. е.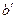 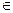B и 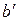= inf B. Но B 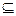A, тогда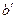 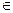A.

Пусть 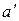- элемент множества А, имеющий наименьшее значение, т.е.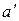 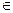А и 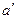= inf A. При этом, если 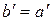, то 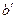= inf A; если 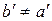, то 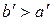= inf A. Таким образом,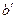 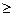inf A или inf B 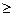inf A.

Аналогично доказывается вторая часть теоремы.