Теорема Г. Кантора

Множество всех действительных чисел интервала 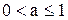несчетно

Доказательство Любое число рассматриваемого интервала представляет собой конечную или бесконечную десятичную дробь вида 0.а₁а₂а₃ … и может быть представлено точкой отрезка вещественной оси. Т.е. теорема утверждает, что множество точек отрезка (0,1] несчетно.

Предположим, что последовательность 0.а₁а₂а₃…представляет собой бесконечный перечень действительных чисел, принадлежащих этому интервалу. Вопрос состоит в том, может или не может подобный перечень содержать все числа этого интервала, т.е. нельзя ли найти число, которое принадлежит этому интервалу, но не входит в указанный перечень чисел. Для того, чтобы найти такое число, запишем все входящие в перечень десятичные дроби одну под другой. Образуем диагональную дробь, указанную стрелками, и заменим в ней каждую из последовательных цифр 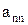на отличную от нее цифру 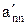так, чтобы при этом не получилась конечная дробь.

. ……….

. ……….

. ……….

. ……….

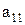
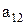
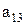
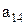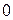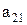
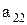
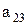
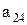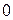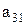
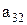
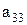
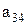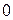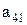
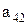
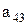
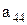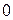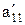
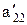
Полученная дробь . 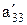… представляет собой действительное число, принадлежащее нашему интервалу, но не входящее в рассматриваемый перечень. Действительно, эта дробь отличается от первой из данных дробей своей первой цифрой после запятой, от второй - своей второй цифрой после запятой, от третьей - третьей цифрой после запятой и т. д. Теорема доказана.

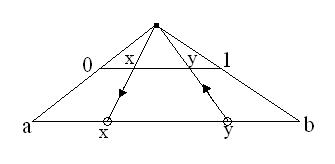
Рассматриваемый интервал (0,1] может быть приведен во взаимно однозначное соответствие с любым другим интервалом (а,b].

Такое взаимно однозначное соответствие можно уста-новить с помощью цен-тральной проекции.

1.13.5 Теорема Кантора – Бернштейна

Пусть А и В – два произвольных множества. Если существует взаимно однозначное отображение f множества А на подмножество В₁ множества В и взаимно однозначное отображение g множества В на подмножество А₁ множества А, то А и В эквивалентны.

1.13.6 Верхняя и нижняя границы множества

Рассматривая подмножество А упорядоченного основного (в частности, универсального) множества I и пусть R – некоторое отношение порядка на I. Если существует такой элемент МÎI, что для всех аÎА справедливо утверждение аRМ, то М называется мажорантой А.

Аналогично, если существует такой элемент mÎI, что для всех аÎА удовлетворяет отношение mRa, то m называется минорантой множества А.

Если мажоранта М множества А принадлежит множеству А, то М называется максимумом множества А (наибольшим элементом множества А). Обозначается следующим образом: maxA=M; 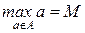. Максимум М единственен. Действительно, предположим противное, что множество А имеет два максимума (М₁ и М₂), тогда условия "(а) (aRM₁) и "(а) (aRM₂) влекут M₁RM₂ и M₂RM₁, следовательно, в силу антисимметричности отношений порядка M₁=M₂.

Если миноранта mÎA, то m называется минимумом множества А (наименьшим элементом). Обозначается: minA=m; 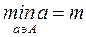. Минимум m единственен.

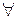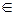Пусть Z – множество вещественных чисел. Верхней границей Z является число H такое, что для любого z Z имеет место z H ( z|z 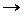Z z 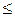H; H – sup Z).

Точной верхней границей или супремумом множества Z, обозначаемой sup Z, называют верхнюю границу, которая не превосходит любую другую верхнюю границу. Множество может иметь только одну точную верхнюю границу.

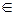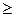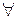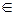Нижней границей множества Z является число L такое, что для любого z Z имеет место z L ( z|z Z ®z 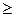L ® inf Z = L).

Точной нижней границей называют нижнюю границу, не меньшую любой другой нижней границы. Нижняя граница обозначается inf Z и называется инфинумом.

Рассмотрим отрезок [a, b], a < b на числовой оси. Основное множество – множество действительных чисел упорядочено отношением “ £ ”. Любое действительное число, большее или равное b, является мажорантой. Множество этих мажорант имеет минимум, равный b, следовательно sup[a, b]=b. Аналогично inf[a, b]=a.

С другой стороны, мажоранта b принадлежит отрезку [a, b], следовательно, число b является максимумом: max[a, b]=b; min[a, b]=a.

Если бы рассматривали интервал (а, b), то а и b являются соответственно минорантой и мажорантой, но не принадлежат интервалу (a, b), поэтому не являются минимумом и максимумом (a, b). Числа а и b и в этом случае являются нижней и верхней границами множества (a, b) соответственно.

Таким образом, если множество мажорант (минорант) в свою очередь имеют минимум (максимум), то этот элемент единственен и соответствует верхней (нижней) границе.1