2.1 Краткие теоретические сведения
2.1.1 Системы счисления
Система счисления – символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
- даёт представления множества чисел (целых или вещественных)
- даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
- отражает алгебраическую и арифметическую структуру чисел.
Системы счисления подразделяются на позиционные, непозиционные и смешанные.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
Каждая позиционная система счисления определяется некоторым целым числом 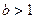 (т. н. основание системы счисления) таким, что b единиц в каждом разряде объединяется в одну единицу следующего по старшинству разряда.
(т. н. основание системы счисления) таким, что b единиц в каждом разряде объединяется в одну единицу следующего по старшинству разряда.
Целое число x в показательной системе счисления представляется в виде конечной линейной комбинации степеней числа b:
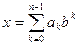 , ,
| (1.1) |
где 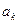 – это целые числа, называемые цифрами, удовлетворяющие неравенству
– это целые числа, называемые цифрами, удовлетворяющие неравенству 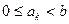 ,
, 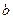 – основание системы счисления,
– основание системы счисления, 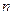 – число разрядов. Каждая степень bk в такой записи называется разрядом, старшинство разрядов и соответствующих им цифр определяется значением показателя k.
– число разрядов. Каждая степень bk в такой записи называется разрядом, старшинство разрядов и соответствующих им цифр определяется значением показателя k.
Наиболее употребляемыми в вычислительной технике позиционными системами являются двоичная, восьмеричная, десятичная и шестнадцатеричная.
2.1.2 Перевод произвольной позиционной системы счисления в десятичную
Если число в b-ричной системе счисления равно 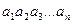 , то для перевода в десятичную систему вычисляется сумма:
, то для перевода в десятичную систему вычисляется сумма:
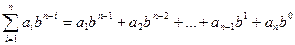 , ,
| (1.2) |
где 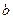 – основание системы счисления, из которой осуществляется перевод.
– основание системы счисления, из которой осуществляется перевод.
2.1.3 Перевод из десятичной в произвольную позиционную систему счисления
Для перевода необходимо делить число с остатком на основание системы счисления до тех пор, пока частное больше основания.
2.1.4 Перевод из двоичной в восьмеричную и шестнадцатеричную системы счисления
Для этого типа операций существует упрощенный алгоритм.
Для восьмеричной – разбиваем число на триплеты, преобразуем триплеты по таблице 1.1.
Таблица 1.1 – Перевод числа из двоичной в восьмеричную систему счисления
| Число в двоичной системе счисления | Число в восьмеричной системе счисления |
Для шестнадцатеричной – разбиваем на квартеты, преобразуем по таблице 1.2.
Таблица 1.2 – Перевод числа из двоичной в шестнадцатеричную систему счисления
| Число в двоичной системе счисления | Число в шестнадцатеричной системе счисления |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
2.1.5 Перевод дробных чисел из произвольной системы счисления в десятичную
Если число в b-ричной системе счисления записано в виде 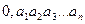 , то для перевода в десятичную систему вычисляется сумма:
, то для перевода в десятичную систему вычисляется сумма:
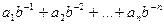 . .
| (1.3) |
2.1.6 Перевод дробных чисел из десятичной системы счисления в произвольную
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основание той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
В общем случае очень редко удаётся завершить перевод дробной части числа из десятичной системы в другие системы счисления, а потому, в подавляющем большинстве случаев, перевод можно осуществить с какой либо долей погрешности. Чем больше знаков после запятой – тем точнее приближение результата перевода к истине.
2.1.7 Операции с числами в произвольных системах счисления
2.1.7.1 Сложение и вычитание
Как в десятичной, так и в любой другой системе при сложении складываются сначала единицы, затем переходят к следующему разряду и т.д. до тех пор, пока не доходят до самого старшего из имеющихся разрядов. При этом необходимо помнить, что всякий раз, когда при сложении в предыдущем разряде получается сумма больше, чем основание системы счисления, или равная ему, надо сделать перенос в следующий разряд.
Вычитание выполняется аналогичным образом. При заеме из старшего разряда, величина заема равна основанию системы счисления.
2.1.7.2 Умножение
Для умножения чисел в различных системах счисления удобно пользоваться таблицами умножения. В каждой клетке такой таблицы стоит произведение чисел, представляющих собой номера строки и столбца, на пересечении которых стоит клетка.
Таблица 1.3 – Таблица умножения для двоичных чисел
Таблица 1.4 – Таблица умножения шестнадцатеричных чисел
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | C | E | 1A | 1C | 1E | |||||||||||
| C | F | 1B | 1E | 2A | 2D | |||||||||||
| C | 1C | 2C | 3C | |||||||||||||
| A | F | 1E | 2D | 3C | 4B | |||||||||||
| C | 1E | 2A | 3C | 4E | 5A | |||||||||||
| E | 1C | 2A | 3F | 4D | 5B | |||||||||||
| 1B | 2D | 3F | 5A | 6C | 7E | |||||||||||
| A | A | 1E | 3C | 5A | 6E | 8C | ||||||||||
| B | B | 2C | 4D | 6E | 8F | 9A | ||||||||||
| C | C | 3C | 6C | 9C | ||||||||||||
| D | D | 1A | 4E | 5B | 8F | 9C | ||||||||||
| E | E | 1C | 2A | 7E | 8C | 9A | ||||||||||
| F | F | 1E | 2D | 3C | 4B | 5A |
Пользуясь такими таблицами, легко перемножить «столбиком» числа, содержащие любое количество разрядов.
 2015-06-26
2015-06-26 211
211







