Классификация суждений

1. Общеутвердительные суждения. Обозначаются они так: .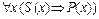

2. Частноутвердительные суждения. Обозначаются следующим образом: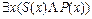

3. Общеотрицательные суждения. Обозначаются они так: Обозначаются они так: .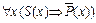

4. Частноотрицательные суждения. Обозначается: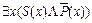

В учебнике для VI класса на основании двух частных примеров делается общий вывод. Учителю же необходимо сде­лать сначала частный выводу только затем можно дать формули­ровку общего заключения, которое будет доказано позже.

Отметим, что для словесного выражения теорем обычно ис­пользуют две формы суждений: категорическую (когда принад­лежность или непринадлежность некоторого признака предмету утверждается независимо от каких бы то ни было условий) и условную (когда истинность суждения ставится в зависимость от определенных условий). Так, например, суждение «Парал­лельный перенос является перемещением» является категориче­ским, в то время как суждение «Если две прямые центрально симметричны, то они параллельны»—условным.

Важнейшими видами сложных суждений являются теоремы и аксиомы (постулаты).

Аксиома (греч. "axioma" — авторитетное предложение «то, что приемлемо») - предложение, принимаемое без доказательства. Определенное число аксиом образует систему отправных, исходных положений некоторой научной теории, лежащую в основе доказательств других положений (теорем) этой теории, в границах которой каждая из аксиом принимается без доказательства. Таково, например, известное положение евклидовой геометрии «Через две точки проходит единственная прямая».

Аксиомы и первичные (неопределяемые) понятия составляют основной фундамент математической теории. К системе аксиом, характеризующих некоторую научную теорию, предъявляются, как известно, требования независимости, непротиворечивости, полноты.

Слово «постулат» происходит от латинского слова "postulatum", обозначающего требование.

Постулат это предложение, в котором выражается некоторое требование (условие), которому должно удовлетворять некоторое понятие или некоторое отношение между понятиями. Нередко постулаты являются частью определения некоторого понятия или некоторой системы понятий. Например, отношение эквивалентности определяется тремя постулатами. Именно для того, чтобы некоторое отношение т, заданное на множестве А, было отношением эквивалентности, должны иметь место следующие свойства:

1) отношение должно быть рефлексивным, т. е.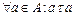

2) отношение должно быть симметричным, т. е.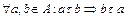

3) отношение должно быть транзитивным, т. е.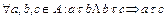

При изучении свойств различных математических объектов (например, фигур - в геометрии, чисел - в арифметике, уравнений - в алгебре) приходится делать те или иные заключения, т. е. на основе понятий того или иного раздела математики строить предложения, истинность которых необходимо обосновать. Математическое предложение, истинность которого устанавливается посредством доказательства (рассуждения), называется теоремой (от греческого слова "theorema" < "theorio" - рассматриваю, обдумываю). В теореме должно быть ясно указано:

1) при каких условиях рассматривается в ней тот или иной объект (условие теоремы);

2) что об этом объекте утверждается (заключение теоремы). Пример. В параллелограмме диагонали, пересекаясь, делятся пополам.

Здесь условие теоремы: р - четырехугольник-параллелограмм, диагонали его пересекаются;

заключение теоремы: q точка пересечения диагоналей делит каждую из них пополам.

Чтобы легче выделить условие и заключение теоремы, ее часто формулируют в виде импликации, применяя логический союз: «если..., то...».

Проиллюстрируем эти виды теорем на следующем примере.

Если четырехугольник—параллелограмм, то.в нем противо­положные стороны попарно конгруэнтны. 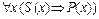- (1)

Если в четырехугольнике противоположные стороны попар­но конгруэнтны, то этот четырехугольник—параллелограмм 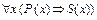- (2).

Если четырехугольник не является параллелограммом, то его противоположные стороны попарно не конгруэнтны. 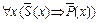- (3).

Если в четырехугольнике противоположные стороны попарно не конгруэнтны, то этот четырехугольник—не параллело­грамм. 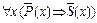- (4).

Нетрудно убедиться, что теоремы (1) и (4) (а также (2) и (3)) равносильны друг другу т. е. если истинна одна, то истинна и другая. Истинность теоремы (1) вовсе не влечет за собой не­пременной истинности теоремы (2), также как и истинность теоремы (3) еще не обеспечивает истинности теоремы (4). Фор­мально этот факт учащиеся усваивают довольно быстро, но тем не менее нередко ссылаются на прямую теорему, имея в виду об­ратную (иной раз не только не доказанную, но даже и не сфор­мулированную). Так, на вопрос «Почему треугольник со сторона­ми, длины которых равны 3, 4 и 5, прямоугольный?» многие отвечают: «По теореме Пифагора», хотя этот факт следует из;теоремы, обратной теореме Пифагора.

: Методика изучения теорем и их доказательств