Доказательством называют конечную последовательность предложений данной теории, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предыдущих предложений этой последовательности по правилам логического вывода.
При введении теорем, как и при введении понятий, используются два метода: конкретно-индуктивный и абстрактно-дедуктивный. (Эти методы широко применяются в дальнейшем и лежат в основе методических схем изучения многих теорем.) В первом случае теорема в готовом виде не сообщается, проводится специальная работа по «подведению» учащихся к теореме, обнаружению соответствующей математической закономерности. Итогом этой работы является формулирование изучаемой теоремы.
Абстрактно-дедуктивный метод введения теоремы начинается с того, что учитель сам формулирует эту теорему, а затем проводится работа по уточнению смысла данной теоремы, ее условия и заключения, построению чертежа и т. д.
Доказательство теоремы представляет собой цепочку рассуждений (силлогизм).
Построение доказательств обычно представляет собой цепочку так называемых силлогизмов – умозаключений, в которых на основании двух категорических суждений (большей посылки и меньшей посылки) выводится третье суждение (вывод заключение).
Рассмотрим доказательство первого признака параллелограмма («Геометрия, 6»): «Если в четырехугольнике противоположные стороны попарно конгруэнтны, то этот четырехугольник — параллелограмм».
1-й силлогизм. Б. П.: если три стороны одного треугольника соответственно конгруэнтны трем сторонам другого треугольника, то такие треугольники конгруэнтны.
М. П.: стороны АВ, ВС и СА треугольника АВС соответственно конгруэнтны сторонам СD, DА и АС треугольника СDА. Заключение: треугольники АВС и СDА конгруэнтны.
2-й силлогизм. Б. П.: в конгруэнтных треугольниках против конгруэнтных сторон лежат конгруэнтные углы.
М. П.: в конгруэнтных треугольниках АВС и СDА стороны АВ и СD конгруэнтны, против них лежат углы 1 и 3. Заключение: углы 1 и 3 конгруэнтны.
3-й силлогизм имеет ту же большую посылку, что и второй, в малой же посылке рассматривается вторая пара сторон и углов, и, следовательно, в заключении утверждается конгруэнтность углов 2 и 4.
4-й силлогизм. Б. П.: если какие-либо два внутренних накрест лежащих угла при пересечении двух прямых третьей конгруэнтны, то эти две прямые параллельны.
М. П.: углы 1 и 3 являются внутренними накрест лежащими при пересечении двух прямых АВ и СD третьей прямой АС. Эти углы конгруэнтны.
Заключение: прямые АВ и СD параллельны.
5-й силлогизм имеет ту же большую посылку, что и четвертый, в меньшей же посылке рассматривается вторая пара углов и вторая пара прямых, в заключении утверждается параллельность прямых ВС и АD.
6-й силлогизм. Б. П.: четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.
М. П.: в четырехугольнике АВСD противоположные стороны попарно параллельны. Заключение: четырехугольник АВСD— параллелограмм.
Теорема доказана.
Доказательства бывают прямые и косвенные. Прямые доказательства, в свою очередь, делятся на синтетические и аналитические.
· I. Рассмотрим синтетический метод доказательства
Исходным моментом синтетического доказательства является условие теоремы. На основе предыдущих предложений и законов логики условие теоремы постепенно преобразуют до тех пор, пока не приходят к заключению. К достоинствам синтетического метода относятся: исчерпывающая полнота, сжатость, краткость (обычно он применяется при изложении уже разработанных математических теорий, известных доказательств или доказательств, отыскание которых не вызывает у учащихся затруднения). Синтетический метод в методическом отношении имеет и свои недостатки. Остается неясным, как можно обнаружить такое доказательство, почему в рассуждениях поступают так, а не иначе; дополнительные построения никак не аргументируются; учащиеся, слушая или читая доказательство, воспринимают его пассивно, соглашаются с истинностью каждого умозаключения и не представляют, в каком направлении должны протекать дальнейшие рассуждения. Этот способ мало способствует самостоятельному открытию доказательства; идея, план рассуждений остаются скрытыми от учащихся.
Пример. Доказать, что если в четырехугольнике противоположные стороны попарно равны, то четырехугольник — параллелограмм. Приведем краткую запись теоремы: 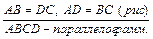 ,
,
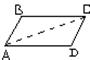
Доказательство. Выполним дополнительное построение: Проведем диагональ АС. Тогда:
1) (АВ=DС, ВС=АD, АС— общая)  (ΔАВС=ΔСDА) (на основании третьего признака равенства треугольников);
(ΔАВС=ΔСDА) (на основании третьего признака равенства треугольников);
2) (ΔАВС=ΔСDA, АВ=DС)  (
(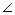 АСВ=
АСВ= 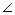 САD);
САD);
3) (ΔАВС=ΔСDA, ВС=AD)  (
(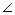 ВAC=
ВAC= 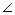 АCD) (на основании определения равенства двух треугольников);
АCD) (на основании определения равенства двух треугольников);
4) п.2  ВС || АD)
ВС || АD)
5) п.3  (АВ || DС) (на основании признака параллельности двух прямых);
(АВ || DС) (на основании признака параллельности двух прямых);
6) (пп. 4 и 5)  (ABCD — параллелограмм) (на основании определения параллелограмма).
(ABCD — параллелограмм) (на основании определения параллелограмма).
Обратите внимание на то, что здесь приводится еще одна форма представления доказательства в виде конечной последовательности предложений.
Компенсировать недостатки синтетического метода помогают следующие методические приемы.
1. Прием формулирования общего замысла (идеи) доказательства.
2. Прием мотивировки дополнительных построений.
3. Прием приведения плана доказательства.
4. Прием проведения доказательства с опорой на краткую его запись.
5. Прием составления блок-схемы доказательства.
6. Прием составления таблицы с двумя параллельными колонками: «Утверждение» и «На основании».
· II. Обратимся к аналитическому методу доказательства.
Восходящий анализ (анализ Паппа). При доказательстве методом восходящего анализа отталкиваются от заключения теоремы и подбирают для него достаточные условия. В символической записи процесс доказательства методом восходящего анализа можно представить следующим образом. Пусть «А  В» —данная теорема. Для заключения В подбираем достаточное условие А1, т. е. такое условие, что А1
В» —данная теорема. Для заключения В подбираем достаточное условие А1, т. е. такое условие, что А1  В. Для А1, в свою очередь, находим достаточное условие А2: А2
В. Для А1, в свою очередь, находим достаточное условие А2: А2  A1 и т. д. Подбор достаточных условий продолжается до тех пор, пока для какого-либо Аi точным условием окажется условие теоремы, т. е. условие А: А
A1 и т. д. Подбор достаточных условий продолжается до тех пор, пока для какого-либо Аi точным условием окажется условие теоремы, т. е. условие А: А  Ai. В итоге доказательство теоремы завершается: А
Ai. В итоге доказательство теоремы завершается: А  Ai, Аi
Ai, Аi  Ai-1, А1
Ai-1, А1  B. Следовательно, А
B. Следовательно, А  B.
B.
Приведем доказательство теоремы: «Если в четырехугольнике противоположные стороны попарно равны, то четырехугольник—параллелограмм» методом восходящего анализа.
1. Для доказательства того, что четырехугольник ABCD является параллелограммом, достаточно доказать, что BC || AD и AB || DC. (A1)
2. Для доказательства параллельности сторон четырехугольника достаточно доказать равенство накрест лежащих углов, образуемых при пересечении двух прямых третьей. (А2)
3. Такие накрест лежащие углы можно получить, если провести диагональ AC:
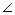 ACB и
ACB и 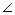 CAD;
CAD; 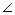 BAC и
BAC и 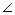 ACD. (А3)
ACD. (А3)
4. Для доказательства равенств 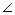 ACB=
ACB= 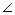 CAD и
CAD и 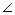 BAC=
BAC= 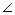 ACD достаточно доказать равенство треугольников АВС и CDA. (A4)
ACD достаточно доказать равенство треугольников АВС и CDA. (A4)
5. Для доказательства равенства треугольников АВС и CDA достаточно установить справедливость равенств: AD=ВС, АВ=DC, AC=AC,a эти равенства выполняются. (A)
Теорема доказана.
Нисходящий анализ (анализ Евклида). При нисходящем анализе рассуждения также начинают с заключения теоремы, однако подбирают уже не достаточные, а необходимые условия. Выведение необходимых условий продолжают до тех пор, пока не придут к очевидному следствию, представляющему собой или условие теоремы, или ранее изученное предложение. Если окажется возможным провести рассуждения в обратном порядке, при котором условие теоремы или очевидное предложение выступают отправной посылкой, то получим искомое доказательство.
Итак, пусть А  B — данная теорема. Допустим, что из заключения теоремы В выводится следствие B1: B
B — данная теорема. Допустим, что из заключения теоремы В выводится следствие B1: B  B1, из B1, в свою очередь,—следствие B2 и т. д.:
B1, из B1, в свою очередь,—следствие B2 и т. д.:
B=B1, B1  B2, …, Bi-1
B2, …, Bi-1  Bi, Bi
Bi, Bi  A. (1)
A. (1)
Если возможно провести рассуждения в обратном порядке:
A  Bi, Bi
Bi, Bi  Bi-1,…, B2
Bi-1,…, B2  B1, B1
B1, B1  B, (2)
B, (2)
то получим доказательство теоремы.
Понятно, что цепочка рассуждений (1) не является доказательством теоремы. Цель ее — чисто методическая: найти доказательство (2).
Если обратиться к рассмотренной выше теореме, то нисходящий анализ может быть проведен следующим образом:
1. Пусть ABCD — параллелограмм. (B)
2. Тогда BC || AD и AB || DC. (B1)
3. Тогда 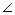 ACB=
ACB= 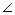 CAD,
CAD, 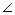 BAC=
BAC= 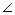 ACD (как накрест лежащие углы при параллельных прямых и секущей). (B2)
ACD (как накрест лежащие углы при параллельных прямых и секущей). (B2)
4. Из равенства этих углов с учетом того, что АС— общая сторона ΔABC и ΔCDA, следует: ΔABC = ΔCDA. (B3)
5. Тогда AD=BC, AB=DC, AC = AC. (A)
Итак, B=B1, B1  B2, B3
B2, B3  A.
A.
Обратимся к косвенному доказательству. В школьной практике обычно оно называется методом от противного. Доказательство теоремы A  B начинают с допущения, что из А не следует В. Тогда имеет место истинность предложения A и ложность предложения В. Из предложения (А и
B начинают с допущения, что из А не следует В. Тогда имеет место истинность предложения A и ложность предложения В. Из предложения (А и 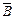 ) выводят следствие В1, из предложения В1 — следствие В2 и так далее, пока не получится следствие Вi,находящееся в противоречии либо с условием теоремы, либо с одним из ранее изученных предложений. Полученное противоречие означает, что допущение
) выводят следствие В1, из предложения В1 — следствие В2 и так далее, пока не получится следствие Вi,находящееся в противоречии либо с условием теоремы, либо с одним из ранее изученных предложений. Полученное противоречие означает, что допущение 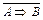 неверно, а, значит, верно предложение А
неверно, а, значит, верно предложение А  В. Следовательно, теорема А
В. Следовательно, теорема А  В доказана.
В доказана.
 2015-07-02
2015-07-02 1514
1514
