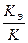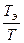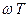Переменная структура системы дает дополнительные возможности получения различных желаемых процессов автоматического управления и регулирования.
В системе (рис.6.3.1) переменная структура создается КЭ.
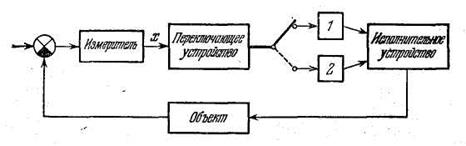
Рис.6.3.1
Рассмотрим переходный процесс (без внешнего воздействия). Пусть измерительное и исполнительное устройства идеальные и вместе с регулируемым объектом описываются передаточной функцией
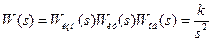 . (6.3.1)
. (6.3.1)
КЭ описывается выражением (6.2.1).
Звенья же 1 и 2 характеризуются коэффициентами усиления k1 и k2 соответственно. Тогда уравнение динамики замкнутой системы при включении звена 1 запишется в виде
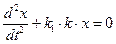 (6.3.2)
(6.3.2)
а при включении звена 2:
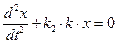 (6.3.3)
(6.3.3)
Каждое из этих уравнений является уравнением неустойчивой автоколебательной системы. Картины фазовых траекторий в соответствии с (6.3.2 и 6.3.3) показаны на рис. 6.3.2, а и б соответственно.
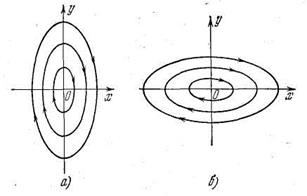
Рис.6.3.2
Обозначим 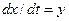 . Введем следующий закон переключений. Пусть звено 1 включается при
. Введем следующий закон переключений. Пусть звено 1 включается при 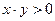 , а звено 2 – при
, а звено 2 – при 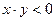 , т. е. имеем уравнения
, т. е. имеем уравнения
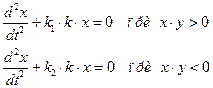
В этом случае в I квадранте фазовой плоскости 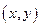 берется дуга эллипса из рис. 6.3.2, а; в IV квадранте - из рис. 6.3..2, б; в III- снова из рис. 6.3.2, а и т. д.
берется дуга эллипса из рис. 6.3.2, а; в IV квадранте - из рис. 6.3..2, б; в III- снова из рис. 6.3.2, а и т. д.
Как видно по рис. 6.3..3, получается затухающий колебательный процесс, т. е. за счет переменности структуры система становится устойчивой.
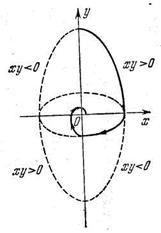
Рис.6.3.3
|
|
Псевдолинейными называют такие нелинейные КУ, у которых эквивалентная передаточная функция, а значит, и коэффициенты гармонической линеаризации зависят только от частоты и не зависят от амплитуды колебаний. Однако, эта зависимость нелинейна в том смысле, что характер ее отличается от частотной зависимости линейных передаточных функций и может быть произвольным, т.е. отсутствует жесткая взаимосвязь между амплитудными и фазовыми характеристиками, которая есть у линейных звеньев. Это достоинство псевдолинейных устройств позволяет корректировать фазовые характеристики независимо от амплитудных и наоборот, что невозможно сделать линейными средствами.
Результат гармонической линеаризации псевдолинейного устройства y=f(x) имеет вид
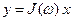 , (6.4.1)
, (6.4.1)
где 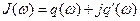 – эквивалентная ПФ псевдолинейного КУ (6.4.2)
– эквивалентная ПФ псевдолинейного КУ (6.4.2)
Е.И. Хлыпало предложил форму представления псевдолинейного устройства в виде эквивалентного инерционного звена
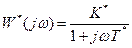
Если 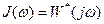 , тогда
, тогда
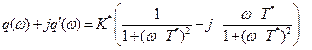 . (6.4.3)
. (6.4.3)
Приравнивая действительные и мнимые части в (6.3.3), получим
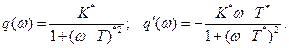 (6.4.4)
(6.4.4)
После преобразований
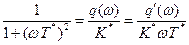 ,
,
получим
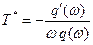 (6.4.5)
(6.4.5)
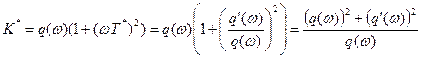 . (6.4.6)
. (6.4.6)
|
|
Цель коррекции – уменьшение инерционности, т.е. уменьшение фазового отставания выходного сигнала от входного. Частотные характеристики апериодического звена имеют вид:
|
|
|





|
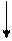
|

|

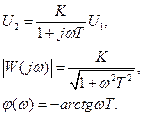
С.А.З. – схема анализа знаков.
|
ПФ формирующих устройств: WK1=1+Ts, WK2=1.
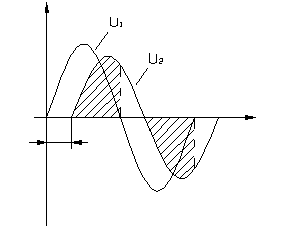
При несовпадении знаков сигналов U 1 и U 2 ключ размыкается и при этом отсекаются хвостовые части выходного сигнала U (рис.6.4.2).
| |||
|
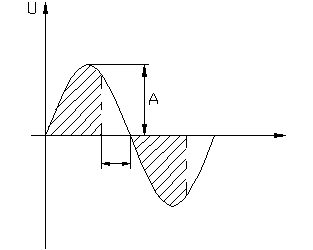
Произведем гармоническую линеаризацию нелинейности (рис.6.4.3).
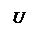 | |||||||
 |
| ||||||
|
Вычисление коэффициентов гармонической линеаризации.
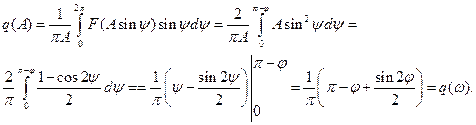 (6.4.7)
(6.4.7)
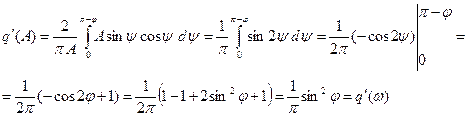 (6.4.8)
(6.4.8)
Из выражений (6.4.7, 6.4.8) видно, что коэффициенты гармонической линеаризации являются функцией фазового сдвига φ(ω), следовательно частоты ω, и не зависят от амплитуды колебаний.
Эквивалентная передаточная функция всего устройства имеет вид
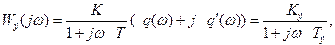 (6.4.9)
(6.4.9)
Рассуждая аналогично предыдущему, найдем параметры Кэ и Тэ.
|
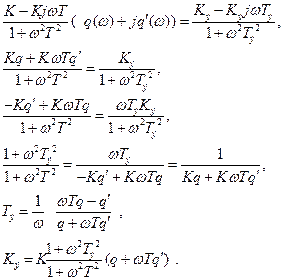
Вместо 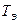 подставим его значение из (6.3.14) и получим
подставим его значение из (6.3.14) и получим
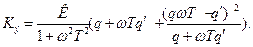 (6.4.15)
(6.4.15)
| |||
| |||
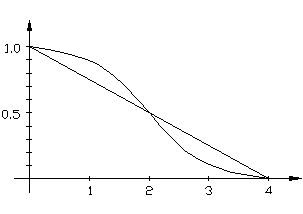
 По формулам (6.4.14, 6.4.15) были рас-считаны относительные значения Кэ и Тэ.
По формулам (6.4.14, 6.4.15) были рас-считаны относительные значения Кэ и Тэ.

|
|
|
Глава 7. Исследование устойчивости нелинейных систем.
7.1. Устойчивость нелинейных систем. Функции Ляпунова А.М.
Уравнение динамики системы n-го порядка при отсутствии внешних воздействий в общем случае описывается следующей системой дифференциальных уравнений в нормальной форме Коши:
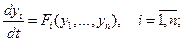 . (7.1.1)
. (7.1.1)
где уi – координаты системы, а Fi – нелинейные функции.
Устойчивость рассматривается как свойство свободного движения системы, вызванного ненулевыми начальными условиями. Решение системы (7.11) представляет собой невозмущенное движение 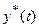 . При изменении начальных условий в системе возникает возмущенное движение. Отклонение возмущенного движения
. При изменении начальных условий в системе возникает возмущенное движение. Отклонение возмущенного движения 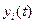 от невозмущённого, определяемого уравнениями системы (7.1.1) при определенных начальных условиях
от невозмущённого, определяемого уравнениями системы (7.1.1) при определенных начальных условиях 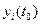 , обозначим через
, обозначим через 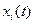
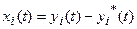 (7.1.2)
(7.1.2)
Тогда уравнение возмущенного движения системы в отклонениях описывается системой дифференциальных уравнений
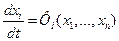 - описывает движение системы. (7.1.3)
- описывает движение системы. (7.1.3)
При этом невозмущенным движением будет x* = 0.
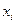 - координаты состояния системы.
- координаты состояния системы.
|
|
|
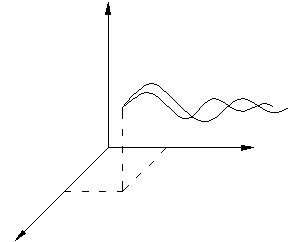
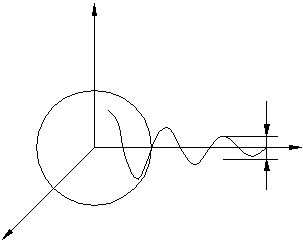 Геометрические представления движений показаны на рис.7.1.1.
Геометрические представления движений показаны на рис.7.1.1. 
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
|
| |||||||||||||||||
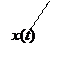 | ||||||||||||||||||
 | ||||||||||||||||||
| ||||||||||||||||||
Устойчивость по Ляпунову: невозмущенное движение 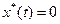 называется устойчивым, если задав трубку сколь угодно малого сечения e, можно в начальный момент времени t 0 подобрать такую область начальных значений d, зависящую от e, что при увеличении времени
называется устойчивым, если задав трубку сколь угодно малого сечения e, можно в начальный момент времени t 0 подобрать такую область начальных значений d, зависящую от e, что при увеличении времени 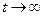 возмущенное движение x (t) не выйдет из трубки сечением e, т.е. при выполнении условия (7.1.4) выполнится условие (7.1.5).
возмущенное движение x (t) не выйдет из трубки сечением e, т.е. при выполнении условия (7.1.4) выполнится условие (7.1.5).

Если при выполнении условия (7.1.4) выполняется (7.1.6), то движение называется асимптотически устойчивым.
Если условие (7.1.6) выполняется при выполнении условия (7.1.7), т.е. при любых начальных отклонениях, движение называют асимптотически устойчивым в целом.
Для нелинейных систем введено понятие абсолютной устойчивости. Под ней понимают асимптотическую устойчивость в целом при любой форме нелинейной характеристики внутри заданного класса нелинейностей.
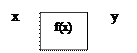
 |  | ||||
|
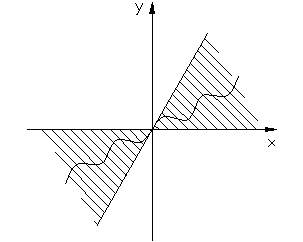
В дальнейшем мы будем рассматривать класс однозначых нелинейных характеристик 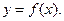
На нелинейность (рис.7.1.2) накладываются следующие ограничения:
– нелинейность должна проходить через начало координат
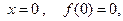
– нелинейная характеристика должна лежать внутри сектора [0,k]
|
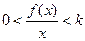 . (7.1.8)
. (7.1.8) Внутри этого сектора она может иметь любой однозначный вид.
 2015-07-04
2015-07-04 712
712