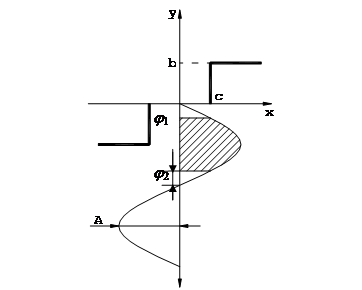
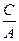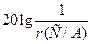 Рассмотрим идеальное 3-х позиционное звено.
Рассмотрим идеальное 3-х позиционное звено.
Нечетно-симметричные характеристики можно интегрировать на интервале 0<φ<π.
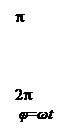
|
|
|
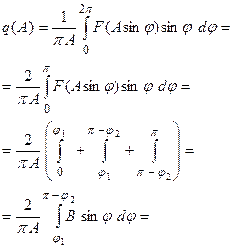 (4.2.1)
(4.2.1) 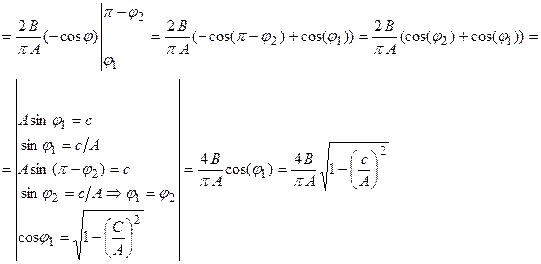 (4.2.2)
(4.2.2)
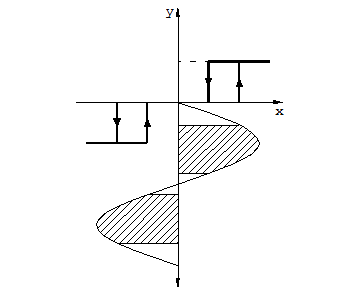
Рассмотрим реальное 3-х позиционное реле.
| |||
|
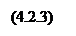
 | |||
|



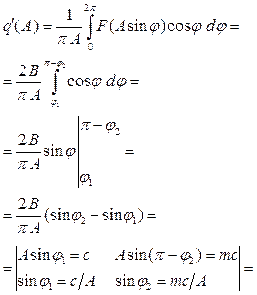
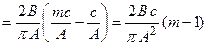
Если m=1 Þ характеристика идеальна; q’(A)=0
Для всех однозначных (беcпетлевых) нелинейностей q’(A)=0, а эквивалентная передаточная функция J(A)=q(A).
Рассмотрим вычисление q(A) для прямой линии: F (x)= kx

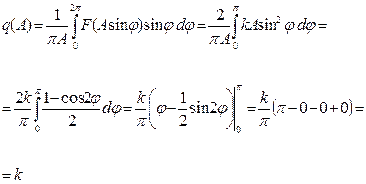
Т.е. гармоническая линеаризация линейной функции дает коэффициент k.
|
их устойчивости
Рассмотрим систему с одной нелинейностью с линейной частью, обладающей фильтрующими свойствами.
 | |||
|
Уравнение нелинейности y = f (x); линейной части для свободного движения: 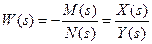 (4.3.1)
(4.3.1)
Уравнение замкнутой системы: 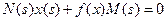
При условии, что x (s) изменяется по гармоническому закону, после гармонической линеаризации можно записать:
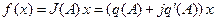 (4.3.2)
(4.3.2)
С учётом (4.3.2) можно записать характеристическое уравнение замкнутой системы в виде 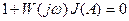 (4.3.3)
(4.3.3)
или после подстановки (4.3.1) в виде
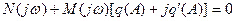 (4.3.4)
(4.3.4)
В выражении (4.3.4), выделяя действительную и мнимую части, получим:
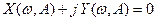 (4.3.5)
(4.3.5)
Приравнивая действительную и мнимую части нулю, получаем систему
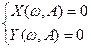 . (4.3.6)
. (4.3.6)
Затем система уравнений (4.3.6) решается относительно двух неизвестных: амплитуды А и частоты w автоколебаний
Если амплитуда и частота получатся комплексными или мнимыми числами, то периодический процесс в системе отсутствует, а если действительными числами – то присутствует.
После определения параметров периодического процесса необходимо проверить его устойчивость. Данная задача в системе, описываемой уравнением высокого порядка весьма сложна, поэтому воспользуемся приближенными методами. Дадим малые отклонения А и w от их значений в периодическом режиме А +Δ А и ω +Δ ω.
Исходное движение 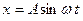 . (4.3.7)
. (4.3.7)
Варьированное движение 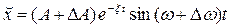 (4.3.8)
(4.3.8)
Выражение (4.3.8) описывает колебательный процесс вблизи исходного периодического режима (4.3.7).
Из анализа (4.3.8) следует: для устойчивости автоколебаний необходимо, чтобы параметры DА и x имели одинаковые знаки. При DА> 0 и x> 0 варьированный процесс будет затухать и стремиться к исходному. При DА< 0 и x< 0 уменьшенный варьированный процесс будет расходиться и стремиться к исходному.
Для увязывания этого условия с параметрами линейной части и нелинейного элемента (для вывода критерия) воспользуемся символической формой записи периодического режима.
Исходный режим (4.3.5) представим в виде:
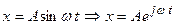 . (4.3.9)
. (4.3.9)
Варьированный режим
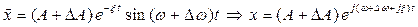 (4.3.10)
(4.3.10)
Аналогично выражению (4.3.5) для варьированного движения можно записать:
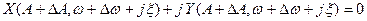 (4.3.11)
(4.3.11)
Разложим (4.3.11) в ряд Тейлора в окрестности А и w, рассмотрим только линейный член и получим:
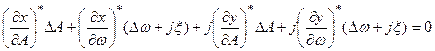 (4.3.12)
(4.3.12)
* – означает подстановку значений А и ω, соответствующих исследуемому автоколебательному режиму.
Выделим в выражении (4.3.12) мнимую и действительную часть, почленно приравняем к 0, исключим из полученных уравнений Δ ω и, разрешив эту систему относительно x, найдем в результате выражение, связывающее параметры ζ и Δ А.
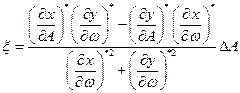 (4.3.13)
(4.3.13)
Поскольку знаменатель функция четная, то знак ζ зависит только от числителя, тогда для совпадения знаков параметров DА и xкритерий устойчивости автоколебаний приобретает вид:
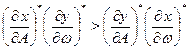 (4.3.14)
(4.3.14)
Для определения автоколебаний алгебраическим методом необходимо:
1) записать характеристическое уравнение замкнутой системы;
2) выделить в нем действительную и мнимую части и приравнять их к нулю;
3) разрешить эту систему относительно амплитуды А и частоты автоколебаний w;
4) найти частные производные действительной и мнимой частей по А и w и подставить в выражения частных производных найденные значения А и w.
5) проверить выполнение условия (4.3.14)
|
и их устойчивости (метод Гольдфарба Л.С.)
Этот метод графоаналитический и представляет собой применение метода гармонической линеаризации к исследованию устойчивости нелинейных систем на основе частотных характеристик (с использованием критерия Найквиста).
Линейная часть (рис.4.3.1)описывается ПФ: 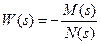 .
.
Уравнение Н.Э y = F (x). При x = Asinωt, после гармонической линеаризации получим: 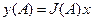 ,
,
где эквивалентная ПФ НЭ
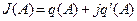 ,
,
коэффициенты гармонической линеаризации
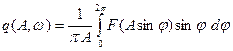
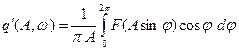 , ωt = φ. Характеристическое уравнение замкнутой линеаризованной системы имеет вид:
, ωt = φ. Характеристическое уравнение замкнутой линеаризованной системы имеет вид:
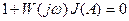 , (4.4.2)
, (4.4.2)
или
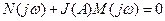 . (4.4.3)
. (4.4.3)
Обычно характеристики нелинейного элемента представляют в нормированном виде:
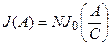 ,
, 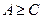 . (4.4.4)
. (4.4.4)
где N- коэффициент, учитывающий параметры нелинейной характеристики.
Например, рассмотрим характеристики идеального трёхпозиционного реле (рис.4.4.1, 4.4.2).
|
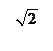
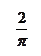
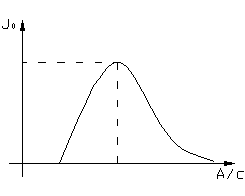
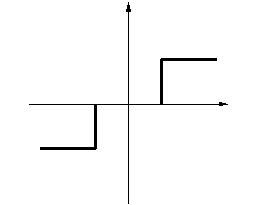


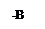
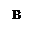
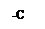
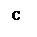
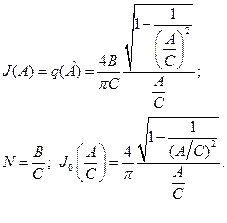
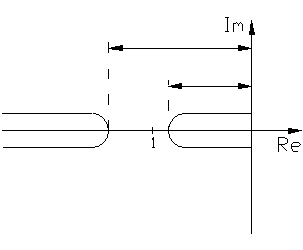
На комплексной плоскости годограф представляет прямую линию на действительной оси т.к. 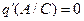 . Поскольку J0(А/С) имеет нелинейный вид (рис.4.4.1), то годограф удобнее представлять в виде (рис.4.4.2).
. Поскольку J0(А/С) имеет нелинейный вид (рис.4.4.1), то годограф удобнее представлять в виде (рис.4.4.2).
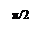
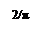
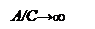
|
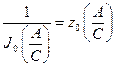 (4.4.5)
(4.4.5) 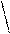 | 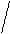 |
| |||||
 | |||||
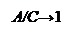 | |||||
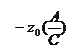
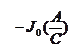
| |||
Характеристическое уравнение в случае нормированной характеристики имеет вид:
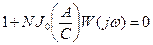 , (4.4.6)
, (4.4.6)
коэффициент N – обычно относят к линейной части.
Для определения автоколебательных режимов характеристическое уравнение (4.4.2) или (4.4.6)
представляют в виде:
а)  б)
б) 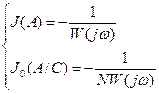 (4.4.7)
(4.4.7)
В соответствии с выражением (4.4.7а) на комплексной плоскости строят два годографа:
- АФХ линейной части W (jω) и годограф обратной амплитудной характеристики нелинейного элемента: – Z (A);
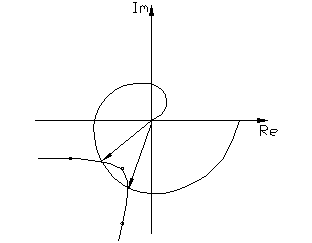 - в случае нормированных нелинейных характеристик NW (jω) и – Z0 (A/C).
- в случае нормированных нелинейных характеристик NW (jω) и – Z0 (A/C).
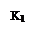
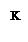
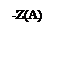
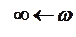
|
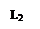
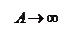
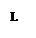
|
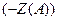 и
и 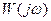 или
или 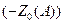 и
и 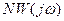 ) пересекаются, то, следовательно, существуют действительные значения амплитуды A и частоты w, удовлетворяющие характеристическому уравнению(4.4.2), и в системе возникают периодические режимы.
) пересекаются, то, следовательно, существуют действительные значения амплитуды A и частоты w, удовлетворяющие характеристическому уравнению(4.4.2), и в системе возникают периодические режимы. Если годографы не пересекаются, то
Рис. 4.4.3 автоколебаний в системе нет.
|
|
|
|
|
|
|
|
|
ПФ разомкнутой линеаризованной системы обозначим через:
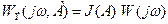 (4.4.8)
(4.4.8)
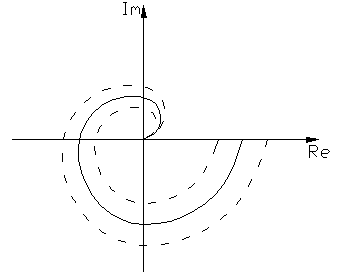
и построим годограф этой функции (рис.4.4.4)
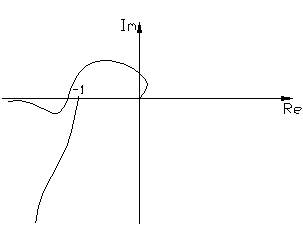
По критерию Найквиста, согласно линейной теории, система находится на границе устойчивости (в ней возникают незатухающий периодический режим), если годограф АФХ Wэ(jω,A) проходит через точку с координатами (-1, j0).
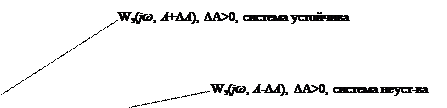 | |||||
| |||||
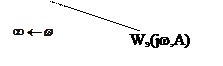 |
Рис.4.4.4
Дадим увеличение амплитуде (А +Δ А). Построим годограф функции Wэ(jω, A +Δ A), он не охватывает точку (–1; j 0), значит, система по Найквисту устойчива, в устойчивой системе амплитуда колебаний уменьшается, следовательно, годограф АФХ вернется в исходное состояние.
Уменьшим амплитуду колебаний (А –Δ А). Годограф АФХ в этом случае охватывает точку (–1; j 0), следовательно, система становится неустойчивой по Найквисту, а в не устойчивой системе амплитуда колебаний увеличивается, и годограф АФХ вернется в исходное состояние.
Таким образом, при изменении амплитуды колебаний в ту или иную сторону годограф АФХ (Wэ(jω, A +Δ A)) возвращается в исходное состояние, что и свидетельствует об устойчивости периодического режима или автоколебаний в данной точке.
Т.о. условие устойчивости автоколебаний можно записать в виде:
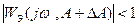 или
или 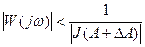 (4.4.9)
(4.4.9)
Вернёмся к рис.4.4.3. Дадим увеличение амплитуде в точке К, (A+DA): K1. Точка K1 годографом АФХ линейной части 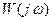 не охватывается, следовательно линеаризованная система устойчива и амплитуда колебаний будет убывать, стремясь к величине А.
не охватывается, следовательно линеаризованная система устойчива и амплитуда колебаний будет убывать, стремясь к величине А.
Дадим уменьшение амплитуды колебаний (A–DA): K2 Годограф АФХ линейной части 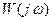 охватывает точку K2, следовательно, система неустойчива, амплитуда колебаний возрастает и стремится к величине А. Поэтому колебания в точке К устойчивы.
охватывает точку K2, следовательно, система неустойчива, амплитуда колебаний возрастает и стремится к величине А. Поэтому колебания в точке К устойчивы.
Рассмотрим точку L. Рассуждая аналогично получим в этой точке неустойчивый периодический режим или неустойчивые автоколебания.
Оценивая свойства нелинейной системы, можно сделать следующий вывод: система устойчива в «малом» и автоколебательна в «большом».
Пример.
Для иллюстрации возможных ситуаций рассмотрим систему (рис.4.3.1) с нелинейностью (рис. 4.4.5) типа люфт или сухое трение. Рассмотрим различные случаи в зависимости от вида годографа линейной части.
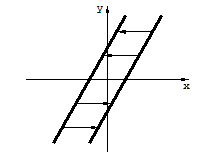


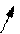


| |||||||||
| |||||||||
| |||||||||
 | |||||||||

|
Случай1.
Годографы не пересекаются, следовательно, автоколебаний нет. Вывод: устойчивая линейная система с учетом нелинейности остается устойчивой.

Случай 2.
Cлучай 2. Годографы пересекаются, в точке К- неустойчивый периодический режим. Вывод: неустойчивая линейная система с учетом нелинейности становится устойчивой в «малом» и неустойчивой в «большом».
Случай 3.
Годографы пересекаются в двух точках.
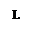 В точке K – неустойчивый периодический режим.
В точке K – неустойчивый периодический режим.
В точке L – устойчивые автоколебания.
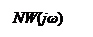
 Устойчивая линейная система с учетом нелинейности становится устойчивой в «малом» и автоколебательной в «большом».
Устойчивая линейная система с учетом нелинейности становится устойчивой в «малом» и автоколебательной в «большом».
 | |||||
 | |||||
 | |||||
 Случай 4.
Случай 4.
Линейная часть имеет астатизм второго порядка (n=2).
Годографы пересекаются в одной точке, автоколебания устойчивы.
|
|
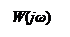 Устойчивая линейная система с учетом нелинейности становится автоколебательной.
Устойчивая линейная система с учетом нелинейности становится автоколебательной. Случай 5.
|
|
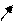 Линейная часть имеет астатизм второго порядка (n=2).
Линейная часть имеет астатизм второго порядка (n=2).
|
Годографы не пересекаются, автоколебаний нет. Неустойчивая линейная система с учетом нелинейности остается неустойчивой.
.
|
 | |||
|
З.Ч.З. – звено чистого запаздывания.
|
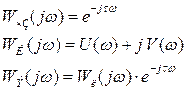
Выражение 4.5.3. представляет собой АФХ линейной части с запаздыванием.
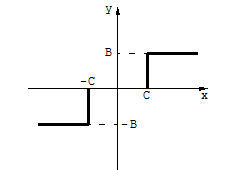
Н.Э. возьмём в виде в виде идеального трёхпозиционного реле (рис. 4.5.2), с эквивалентной ПФ
|
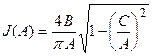 (4.5.4)
(4.5.4)
|
 |
|
|
|
|
|

|
| ||||||||||||||||
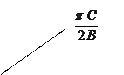 | ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
 | ||||||||||||||||
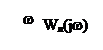 | ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
 | ||||||||||||||||
Для исследования автоколебаний характеристические уравнения систем с запаздыванием и без него представим в виде
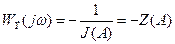 ;
; 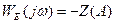 (4.5.5)
(4.5.5)
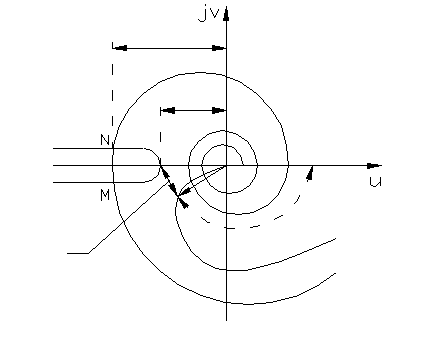
Если годографы Wэ(jω) и -z(A) пересекаются, то имеются автоколебания. При достаточно малом запаздывании кривые не пересекутся и автоколебаний не будет. Критическое время τк запаздывания можно найти без построения годографа Wэ(jω), а только по кривым Wл(jω) и
-z(A), что гораздо проще. Поскольку в критическом случае кривая Wэ(jω) проходит через крайнюю правую точку кривой -z(A), то можно записать равенство 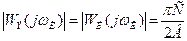 . Из этого выражения можно найти критическую частоту ωк. Учитывая, что в этой точке фазовый сдвиг равен –π, то из выражения
. Из этого выражения можно найти критическую частоту ωк. Учитывая, что в этой точке фазовый сдвиг равен –π, то из выражения 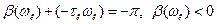 , найдем τк
, найдем τк
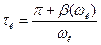 .
.
·
|
 если t<tk – автоколебаний нет
если t<tk – автоколебаний нет ·
|
|
|
4.6.
|
автоколебательных режимов.
 |
После гармонической линеаризации характеристическое уравнение имеет вид:
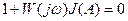 . (4.6.1)
. (4.6.1)
Преобразуем его к виду
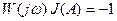 . (4.6.2)
. (4.6.2)
АФХ линейной части и НЭ имеют вид:
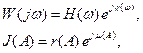 (4.6.3)
(4.6.3)

Учитывая, что в соответствии с формулой Эйлера
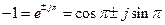 ,
,
выражение (4.6.2) можно записать в виде
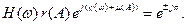 (4.6.4)
(4.6.4)
Приравнивая в правой и левой частях значения модулей и аргументов, получим
уравнение гармонического баланса фаз и амплитуд:
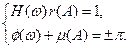 (4.6.5)
(4.6.5)
Для перехода к логарифмической форме запишем:
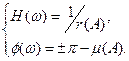 (4.6.6)
(4.6.6)
В логарифмическом виде
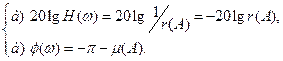 (4.6.7)
(4.6.7)
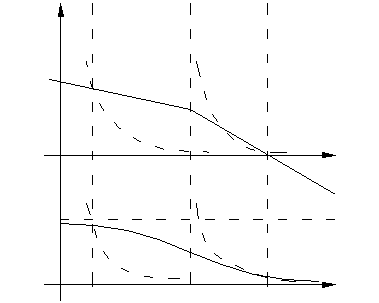
Выражение (4.6.7) показывает, что при одновременном выполнении условий а) и б) в САУ возможны автоколебания. Одновременность выполнения уравнений а) и б) состоит в том, что точки пересечения логарифмических амплитудных характеристик 20lg H (ω) – линейной части и 20lg(1/ r (A)) – нелинейного элемента должны лежать на одной вертикали с точками пересечения фазовых характеристик 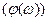 – линейной части и
– линейной части и 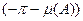 – нелинейного элемента.
– нелинейного элемента.
С помощью графического решения уравнений (4.6.7) можно найти частоту и амплитуду автоколебаний. При этом возможны два метода.
|
Шаблоны приведены, например, в (Атлас по ТАУ, под ред Ю.И.Топчеева).
Рассмотрим применение метода на примере линейной части с ПФ
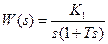 , (4.6.8)
, (4.6.8)
и НЭ типа – люфт (рис. 4.6.1б). Шаблон люфта имеет вид (рис.4.6.1а):
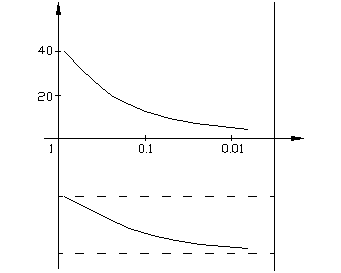
|
| |||||
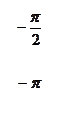 | |||||
| |||||
 |
| ||||||
|
| |||||
|
Шаблон строится в том же масштабе, что и ЛЧХ линейной части. Затем шаблон накладывается на ЛЧХ линейной части так, чтобы совпали оси абсцисс и, затем, перемещается вдоль оси частот и при этом определяется точка пересечения 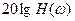 и
и 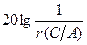 ,
, 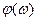 и
и 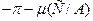 , лежащие на одной вертикали.
, лежащие на одной вертикали.
Если точки пересечения амплитудных и фазовых характеристик находятся на одной вертикали, то автоколебания системы возможны, если нет, то в системе нет автоколебаний.
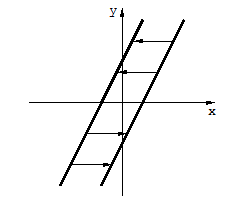
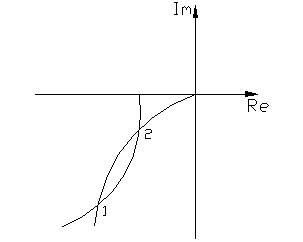
Из рис. 4.6.2а видно, что возможны два случая подобной ситуации. Для вывода критерия определения устойчивости автоколебаний по логарифмическим характеристикам рассмотрим комплексную плоскость (рис.4.6.2б), на которой построены годограф АФХ W(jω) линейной части и годограф 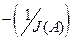 нелинейного элемента. Наблюдаем также две точки пересечения. В соответствии с критерием устойчивости автоколебаний делаем вывод, что в т.1 колебания неустойчивые, а в т.2-устойчивые. В т.2 амплитуда и частота колебаний больше значений соответствующих переменных в т.1.
нелинейного элемента. Наблюдаем также две точки пересечения. В соответствии с критерием устойчивости автоколебаний делаем вывод, что в т.1 колебания неустойчивые, а в т.2-устойчивые. В т.2 амплитуда и частота колебаний больше значений соответствующих переменных в т.1.
Анализируя рис.4.6.2а, можно сформулировать следующий критерий.
Для определения устойчивости автоколебаний в системе с неоднозначным нелинейным элементом необходимо дать приращение амплитуде колебаний.
Если с ростом амплитуды 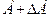 , точка пересечения амплитудных характеристик
, точка пересечения амплитудных характеристик 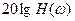 и
и 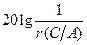 , лежащая на одной вертикали с точкой пересечения фазовых характеристик
, лежащая на одной вертикали с точкой пересечения фазовых характеристик 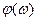 и
и 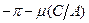 , перейдёт в область над ЛАХ 20lgH(ω), то колебания устойчивы, а если в область под ЛАХ 20lgH(ω) – то неустойчивы.
, перейдёт в область над ЛАХ 20lgH(ω), то колебания устойчивы, а если в область под ЛАХ 20lgH(ω) – то неустойчивы.
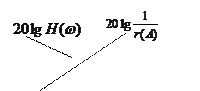 | |||||
| |||||
| |||||
|
| ||||||
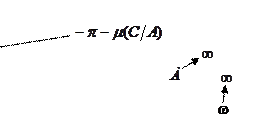 | |||||||
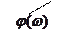 | |||||||
В соответствии с критерием частоте ω 2 соответствуют колебания устойчивые; а частоте ω 1 – неустойчивые.
|
Логарифмические характеристики линейной части и нелинейного элемента строятся раздельно. Причем масштаб по оси ординат должен совпадать, а по оси абсцисс необязательно.
Очевидно, что сразу угадать решение не удастся. Поэтому делают попытки, показанные штриховыми линиями. Последние точки этих пробных прямоугольников М и М1 не попадают на фазовую характеристику нелинейности. Но если они расположены по обе стороны характеристики, как показано на рис. 4.6.3, то решение находится интерполяцией – путем проведения прямой ММ1.

В системе с неоднозначной нелинейностью устойчивые автоколебания возникают в том случае, если с ростом амплитуды колебаний 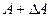 точки пересечения характеристик
точки пересечения характеристик 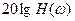 и
и 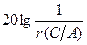 , лежащие на одной вертикали с точками пересечения
, лежащие на одной вертикали с точками пересечения 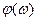 и
и 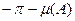 , находятся над ЛАХ линейной части, а если под ЛАХ линейной части – тогда автоколебания неустойчивые.
, находятся над ЛАХ линейной части, а если под ЛАХ линейной части – тогда автоколебания неустойчивые.
|
|
Для однозначных линейных характеристик 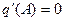 и, следовательно,
и, следовательно, 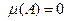 . Уравнение баланса фаз и амплитуд упрощается:
. Уравнение баланса фаз и амплитуд упрощается:
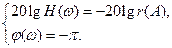 (4.6.9)
(4.6.9)
Автоколебания возможны только в тех точках, где ФЧХ линейной части 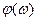 пересекает линию
пересекает линию 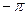 ; если
; если 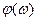 не пересекает линию
не пересекает линию 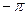 , то автоколебаний нет.
, то автоколебаний нет.
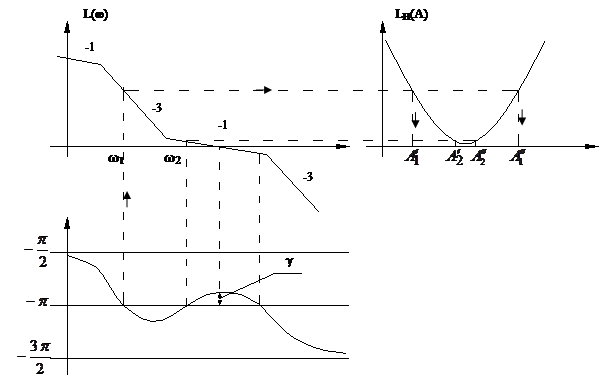
Решение показано на рис. 4.6.4, где обозначено: 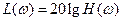 - ЛАХ линейной части,
- ЛАХ линейной части, 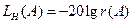 - ЛАХ нелинейного элемента.
- ЛАХ нелинейного элемента.
 | |||
|
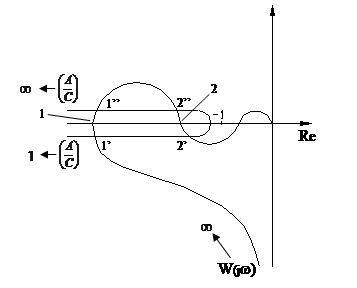
Согласно линейной теории система устойчива, так как имеется запас по фазе γ. Однако на частотах ω1 и ω2 выполняются условия (4.6.9) баланса фаз и амплитуд, поэтому возможны автоколебания с амплитудами 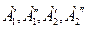 . Для нахождения устойчивых колебаний перейдем к комплексной плоскости. В соответствии с критерием получим две точки неустойчивых колебаний и две точки устойчивых колебаний.
. Для нахождения устойчивых колебаний перейдем к комплексной плоскости. В соответствии с критерием получим две точки неустойчивых колебаний и две точки устойчивых колебаний.
|
В точках 1’(ω1, 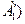 , 2’’
, 2’’ 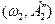 – неустойчивые колебания.
– неустойчивые колебания.
В точках 1’’ 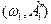 , 2’
, 2’ 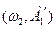 – устойчивые колебания.
– устойчивые колебания.
|
автоколебания будут устойчивы, если в точке выполнения баланса фаз и амплитуд дополнительно выполняется условие:
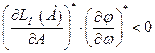 , (4.6.10)
, (4.6.10)
т.е. в рассматриваемой точке угловые коэффициенты наклона ЛАХ НЭ и ФЧХ линейной части должны быть разных знаков.
|
|
|
|
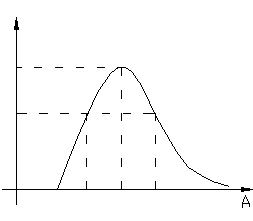
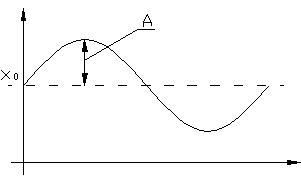 Несимметричные колебания- периодические колебания с постоянной составляющей (рис.4.7.1)
Несимметричные колебания- периодические колебания с постоянной составляющей (рис.4.7.1)
В этом случае входная величина х НЭ ищется в виде:
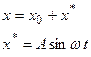 (4.7.1)
(4.7.1)
|
Причин возникновения несимметричных колебаний в общем случае три:
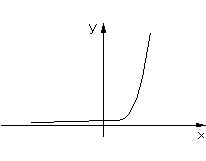 1. Несимметричность нелинейных характеристик;
1. Несимметричность нелинейных характеристик;
|
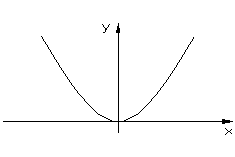 2. Четная симметричность нелинейных характеристик.
2. Четная симметричность нелинейных характеристик.
|
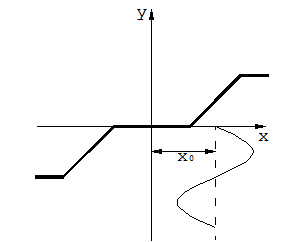 3. Внешнее воздействие с постоянной составляющей;
3. Внешнее воздействие с постоянной составляющей;
|
Пусть нелинейность имеет вид: 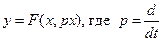 . (4.7.2)
. (4.7.2)
Уравнение гармонической линеаризации НЭ принимает вид:
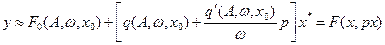 ; (4.7.3)
; (4.7.3)
где коэффициенты гармонической линеаризации определяются по формулам
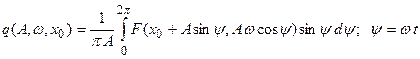 , (4.7.4)
, (4.7.4)
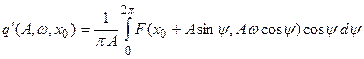 , (4.7.5)
, (4.7.5)
а постоянная составляющая
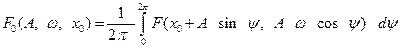 (4.7.6)
(4.7.6)
где x 0 – постоянная составляющая, q и q' – коэффициенты гармонической линеаризации
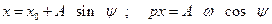 .
.
В отличии от симметричных колебаний, при несимметричных колебаниях коэффициенты гармонической линеаризации зависят не только от амплитуды и частоты колебаний, но и от постоянного смещения x 0.
 2015-07-04
2015-07-04 3081
3081

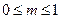
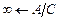
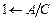
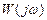
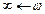
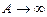
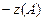
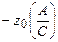
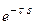 Wл(s)
Wл(s) 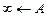
 АN
АN