Свойства плотности распределения

1. Плотность распределения случайной величины неотрицательна 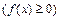при всех значениях .

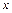2. Условие нормировки:

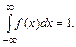(2.11)

Геометрический смысл условия нормировки: площадь под кривой плотности распределения равна единице.

3. Вероятность попадания случайной величины 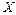в промежуток от 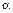до 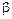может быть вычислена по формуле

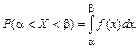(2.12)

Геометрически вероятность попадания непрерывной случайной величины 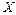в промежуток 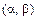равна площади криволинейной трапеции под кривой плотности распределения, опирающейся на этот промежуток.

4. Функция распределения выражается через плотность следующим образом:

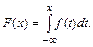(2.13)

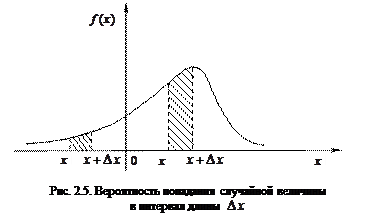
Значение плотности распределения в точке 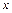не равно вероятности принять это значение, для непрерывной случайной величины речь может идти только о вероятности попадания в заданный интервал. Пусть 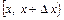— интервал произвольно малой длины 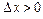. Вероятность попадания случайной величины в этот интервал приближенно равна произведению значения плотности распределения в точке 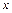на длину этого интервала: 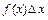, то есть вероятность пропорциональна длине интервала, причем коэффициент пропорциональности равен значению плотности распределения в точке 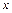(рис. 2.5).

Что происходит с функцией распределения случайной величины при преобразовании самой случайной величины? Ответим на этот вопрос для линейного преобразовании.

Пусть случайная величина 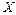имеет функцию распределения 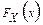. Какую функцию распределения имеет случайная величина ()?

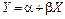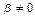По определению функции распределения 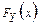= = 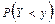= = 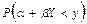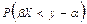. Если 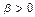, то 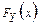= = = 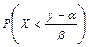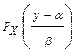. Если 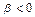, то 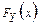= = 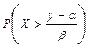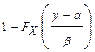. Нами доказана теорема о линейном преобразовании случайной величины.

Теорема 1. Пусть случайная величина 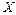имеет функцию распределения 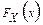. Тогда случайная величина 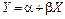(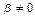) имеет функцию распределения =

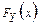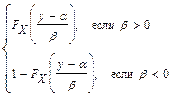
Теорема 2. Пусть случайная величина 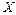имеет плотность распределения 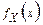. Тогда случайная величина 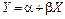(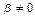) имеет плотность распределения =

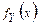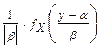
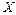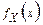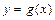Теорема 3. Пусть случайная величина имеет плотность распределения , а непрерывная, кусочно-монотонная, дифференцируемая функция.. Тогда случайная величина 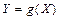имеет плотность распределения

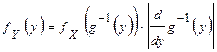
Числовые характеристики непрерывной случайной величины находятся по формулам, похожим на формулы для дискретной случайной величины, но везде знак суммы заменяется на знак интеграла, а вероятность 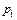на дифференциальный элемент вероятности .

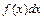Математическое ожидание непрерывной случайной величины равно

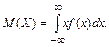(2.14)

Дисперсия непрерывной случайной величины есть

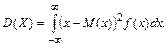(2.15)

Все свойства математического ожидания и дисперсии, сформулированные для дискретных случайных величин, сохраняются и для непрерывных случайных величин.

В качестве примера непрерывной случайной величины рассмотрим случайную величину 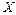, равномерно распределенную на интервале 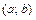. Говорят, что случайная величина 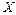равномерно распределена на промежутке 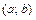, если ее плотность распределения непостоянна на этом промежутке:

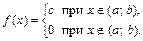
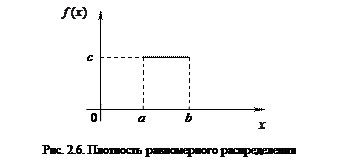
Из условия нормировки (2.11) определим значение константы 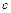. Площадь под кривой плотности распределения должна быть равна единице, но в нашем случае — это площадь прямоугольника с основанием 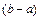и высотой 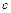(рис. 2.6).

Отсюда находим значение постоянной :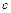

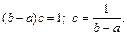
Итак, плотность равномерно распределенной случайной величины равна

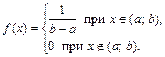
Найдем теперь функцию распределения по формуле (2.13):

1) для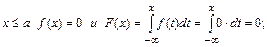

2) для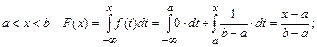

3) для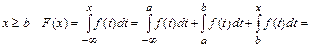

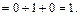
Таким образом,

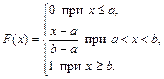
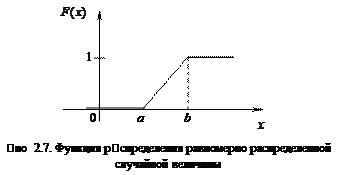
Функция распределения непрерывна и не убывает (рис. 2.7).

Найдем математическое ожидание равномерно распределенной случайной величины по формуле (2.14):

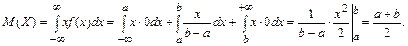Дисперсия равномерного распределения рассчитывается по формуле (2.15) и равна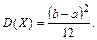

Важным примером непрерывной случайной величины является нормально распределенная случайная величина. Говорят, что случайная величина 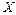имеет нормальное распределение с параметрами 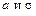, если ее плотность распределения задается формулой:

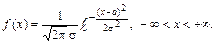
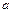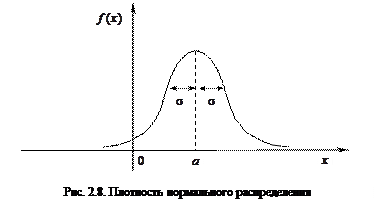
Параметр характеризует положение графика функции на числовой оси, параметр 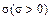— степень сжатия или растяжения графика плотности (рис. 2.8).

Математическое ожидание нормально распределенной случайной величины равно 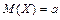, дисперсия .

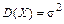Нормальное распределение относится к числу наиболее распространенных и важных, оно применяется для приближенного описания многих случайных явлений. Например, с помощью нормального распределения описывают рассеяние снарядов при стрельбе по цели; отклонение фактического размера изделия от заданного; оно применяется и во многих других ситуациях, когда на интересующий нас признак действует большое количество независимых случайных факторов. С причиной этого мы познакомимся в разделе 4.2.