Коэффициент отражения.
Коэффициент бегущей волны (КБВ).
Коэффициент стоячей волны (КСВ).
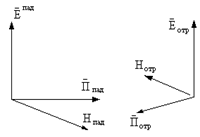
Т.к. в одномодовой линии передачи подающая и отраженная волны имеют одинаковую структуру можно записать следующим соотношением
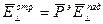 1
1
,где 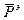 это коэффициент отражения электрического поля, зависящий от одной координаты (Z). Полагая, в соответствии с рисунком, что падающие и отраженные волны имеют нулевое значение фазы при Z=0.
это коэффициент отражения электрического поля, зависящий от одной координаты (Z). Полагая, в соответствии с рисунком, что падающие и отраженные волны имеют нулевое значение фазы при Z=0.
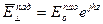 2
2
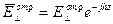 3
3
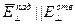 Подставляя (2) и (3) в (1) получим
Подставляя (2) и (3) в (1) получим 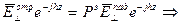
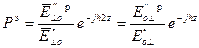
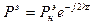
 где Рн -это коэффициент отражения в сечении, где включена нагрузка (Z=0).
где Рн -это коэффициент отражения в сечении, где включена нагрузка (Z=0). 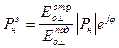
 |
Можно ввести коэффициент отражения по магнитному полю для этого надо воспользоваться
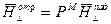
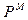 - коэффициент отражения магнитного поля.
- коэффициент отражения магнитного поля. 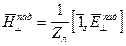
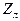 - характеристическое сопротивление соответствующего типа волны.
- характеристическое сопротивление соответствующего типа волны.
В дальнейшем будем пользоваться коэффициентом отражения только по электрическому полю. В произвольном сечении ЛП конечной длины результирующее поле представляет собой суперпозицию подающей и отраженной волн.
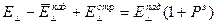 6
6
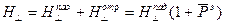 7
7
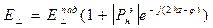 8
8
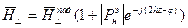 9
9
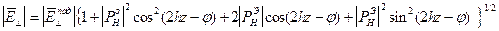

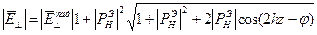 10
10
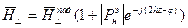 9
9
(10,11) пронормируем относительно Епад
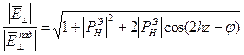 12
12
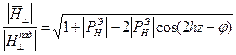 13
13
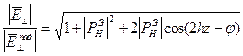
Из (12) следует, что min значение нормиров. напряжен. Есть 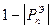
Cos (2hzn - j) = -1 2hz=(2n -1)+j 14
n коорд. min

 координата max
координата max 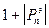 определяется cos. (2hzn - j) = 1 Þ
определяется cos. (2hzn - j) = 1 Þ
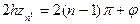 15
15
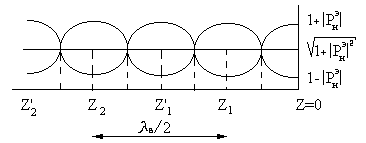 |
где n-координата максимума. Индексация min (узлов) и max (пучностей) ведется
от координаты Z=0.Расстояние
между соседним min или max
равно 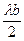 .
.
Из соотношения(14) можно
определить фазу коэффициента
отражения от нагрузки, если
координата min 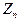 (например, из экспериментальных измерений).
(например, из экспериментальных измерений).
(14)  Þ j =
Þ j = 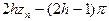 16
16
(15) Þ 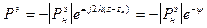
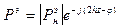
Аналогичным образом фаза нагрузки может (17) быть определена по max.
(15)  Þ j =
Þ j = 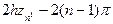
(16) 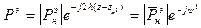 18
18
Отношение min напряж. или магнитного поля к max называется коэффициентом бегущей волны.

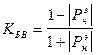 19
19
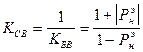 20
20
Наряду с коэффициентом отражения эти два коэффициента также характеризуют режим распространения волны в линии передач конечной длины.
В том случае, когда коэффициент отражения от нагрузки =0
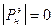
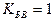
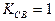 при
при 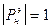
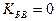
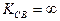
 2015-07-04
2015-07-04 1010
1010







