 Эквивалентное сопротивление длинной линии в некотором сечении определяются как отношение полного напряжения к полному току
Эквивалентное сопротивление длинной линии в некотором сечении определяются как отношение полного напряжения к полному току 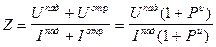 1
1
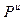 -коэффициент отражения по напряжению
-коэффициент отражения по напряжению 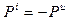
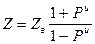 2
2
,где 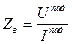 -волновое сопротивление длинной линии.
-волновое сопротивление длинной линии.
 Разделив правую и левую часть на Zв определим нормированное сопротивление в ЛП
Разделив правую и левую часть на Zв определим нормированное сопротивление в ЛП 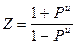 3
3
 Аналогичным образом, используя (3) можно вывести понятие нормированного эквивалентного сопротивления произвольной ЛП.
Аналогичным образом, используя (3) можно вывести понятие нормированного эквивалентного сопротивления произвольной ЛП.
Полагая, что 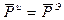
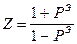 4.
4.
В режиме бегущей волны 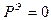 и Z=1 в произвольном сечении произвольной волны. Во всех сечениях произвольной ЛП в точках max или min напряженности электрического поля, эквивалентное нормированное сопротивление является чисто активной величиной.
и Z=1 в произвольном сечении произвольной волны. Во всех сечениях произвольной ЛП в точках max или min напряженности электрического поля, эквивалентное нормированное сопротивление является чисто активной величиной.
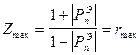
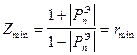
Вспоминая выражения для КБВ и КСВ, видим, что в точках max rmax=KCB,а в min rmin=KБB В соответствии с (4) и общим значением 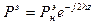 можно получить
можно получить 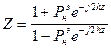

Об изменении нагрузки в конце линии можно судить по комплексному коэффициенту отражения это позволяет каждому значению его в линии передач поставить некоторое эквивалентное сопротивление в конце линии.
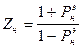 /z=о 6
/z=о 6
Соотношение (6) определяет сопротивление в конце линии, которое называют эквивалентное нормированное сопротивление нагрузки. Выразим из (6) 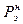 через
через 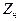 .
. 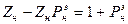 Þ
Þ 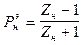 7
7
Подставим (7) в(5)

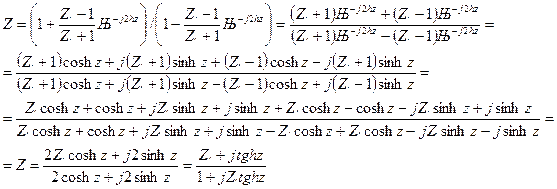
сопротивление 
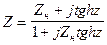 8
8
 |
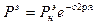 трансформация к.о.
трансформация к.о.
сопротивления в любой точке, зная 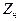 и расстоянию Z
и расстоянию Z
Величина обратная нормированному эквивалентному сопротивлению на нормированный эквивалент проводимости 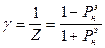
Величина обратная нормированному эквивалентному сопротивлению нагрузки называется нормированной эквивалентной проводимостью.
 2015-07-04
2015-07-04 2883
2883








