СПЕКТРЫ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Комплексную форму математической модели периодического негармонического сигнала получим, представив гармоники в комплексной форме
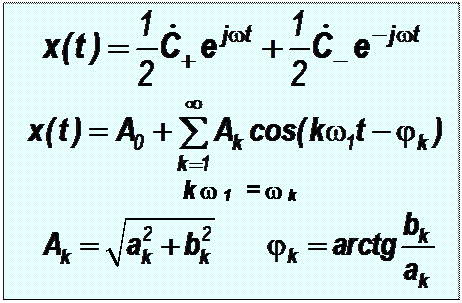 x(t)=A0 +
x(t)=A0 + 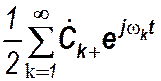 +
+ 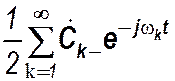 ,
,
а после внесения постоянной составляющей под знак суммы слагаемым при k = 0 в более компактном виде -
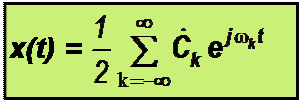
Умножим обе части равенства на 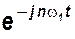 и проинтегрируем в интервале (- Т/2, Т/2):
и проинтегрируем в интервале (- Т/2, Т/2):
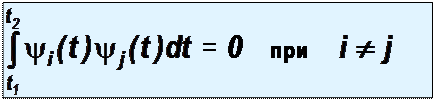
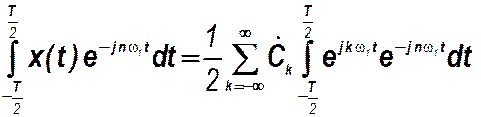
В правой части все слагаемые суммы, кроме одного при n=k,
Обращаются в нуль в силу ортогональности экспоненциальных функций в указанном диапазоне, т.е.
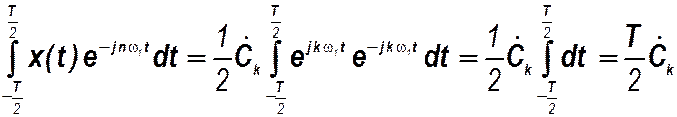
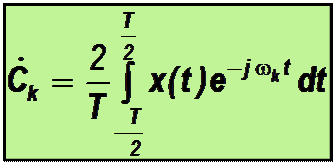
.Поэтому комплексные амплитуды гармоник сигнала определяются по формуле
С учётом формул Эйлера и формул для расчёта коэффициентов обобщённого тригонометрического ряда Фурье составляющие комплексных амплитуд находятся как
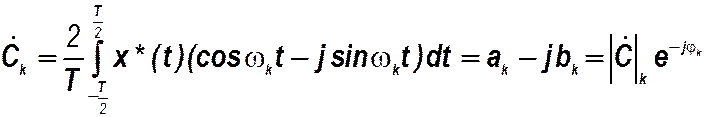 ,
,
где 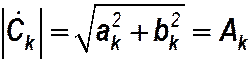 и
и 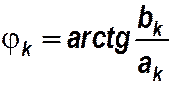
Множество частотных составляющих с w k = k w 1=2 p k/Т при k =0,1,2,…,∞ образуют в совокупности спектр периодического сигнала. Частоты элементарных сигналов – простейших периодических сигналов-гармоник – строго привязаны к периоду конкретного сигнала(постоянная составляющая является частным случаем гармоники с w 0 = 0 и j 0 = 0). А варьируемые индивидуальные значения параметров Аk и j k обеспечивают разнообразие форм получаемых сигналов. Частотное представление периодич. сигнала сводится к указанию его амплитудно-частотной характеристики Ak ( w), называемой спектром амплитуд, и фазочастотной характеристики jk (w) - спектра фаз.
В практических приложениях спектрального представления сигналов основное внимание уделяется амплитудным спектрам. Поэтому в дальнейшем мы будем рассматривать именно спектры амплитуд.
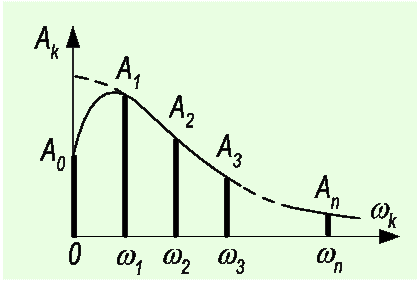
Графически спектры амплитуд и фаз ПНС представляются в виде совокупности бесконечного числа вертикальных линий при частотах 0; ±w 1; ±w 2;... (линейчатый спектр). Гармоники сигнала образуют бесконечное, но счетное множество, в силу чего спектры амплитуд и фаз оказываются дискретными и бесконечными.
 Основная спектральная характеристика периодического сигнала – комплексный спектр – получается заменой wk на текущее значение частоты w:
Основная спектральная характеристика периодического сигнала – комплексный спектр – получается заменой wk на текущее значение частоты w:
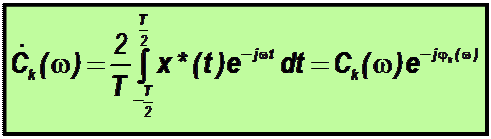 .
.
Кривая, соединяющая концы спектральных линий, называется огибающей спектра амплитуд. Уравнение её даёт зависимость модуля от частоты 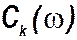 для всех частот, кроме
для всех частот, кроме 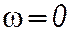 , при которой получается вдвое большее значение. Огибающая спектра амплитуд может иметь волнообразный характер и даже спадать до нуля, если отдельные гармоники отсутствуют.
, при которой получается вдвое большее значение. Огибающая спектра амплитуд может иметь волнообразный характер и даже спадать до нуля, если отдельные гармоники отсутствуют.
Зависимость аргумента от частоты j k (w) дает уравнение огибающей спектра фаз.
Основные отличительные признаки и особенности периодических сигналов и их спектров:
· Любые значения амплитуд сигнала повторяются с постоянным периодом Т на бесконечно-большом интервале времени;
Это в определённой мере противоречит представлению о реальном сигнале, но использовать такую модель допустимо, если длительность периодического сигнала t? Т; в противном случае переходят к модели непериодического сигнала;
· Спектры амплитуд и фаз дискретны, т.е. спектр существует не на всей бесконечной шкале частот, а только в отдельных точках;
· Спектры упорядочены – спектральные линии располагаются только при частотах, кратных основной частоте w 1=2 p / Т;
· Амплитуды гармоник затухают с возрастанием частоты, что следует из сходимости ряда Фурье; при волнообразном характере огибающей наблюдается затухание каждой последующей «волны».
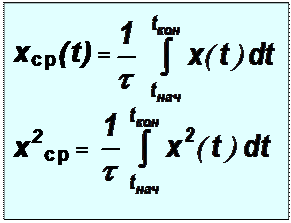 · При определении числовых характеристик периодического сигнала бесконечной продолжительности (tнач=- ∞, t кон=+∞) используют следующий прием: рассматривают вначале отрезок сигнала с N периодами (t =NT), а затем осуществляют предельный переход при N ®∞. Тогда при полной повторяемости формы в каждом периоде среднее значение сигнала находится как
· При определении числовых характеристик периодического сигнала бесконечной продолжительности (tнач=- ∞, t кон=+∞) используют следующий прием: рассматривают вначале отрезок сигнала с N периодами (t =NT), а затем осуществляют предельный переход при N ®∞. Тогда при полной повторяемости формы в каждом периоде среднее значение сигнала находится как
x ср 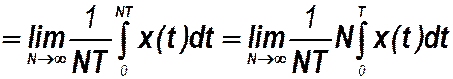
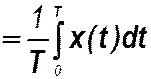 .
.
Аналогично находится среднее квадрата периодического сигнала
x ср 2 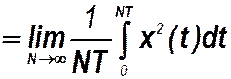
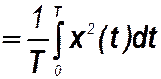 .
.
Таким образом, числовые характеристики периодического сигнала бесконечной продолжительности совпадают с его числовыми характеристиками за период.
Числовые характеристики простейшего периодического сигнала – гармонического - известны
среднее значение® x ср 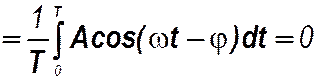 (определяется средним значением cos);
(определяется средним значением cos);
среднее квадрата® x ср 2 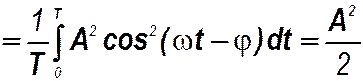 .
.
С учётом этого для периодического негармонического сигнала можнопоказать, что
x ср 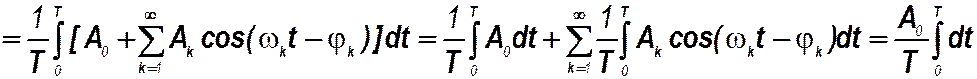
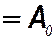 .
.
т.е. среднее значение совпадает с величиной постоянной составляющей.
Определим среднее квадрата (среднюю мощность) периодического сигнала.
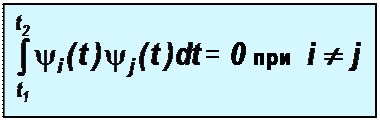
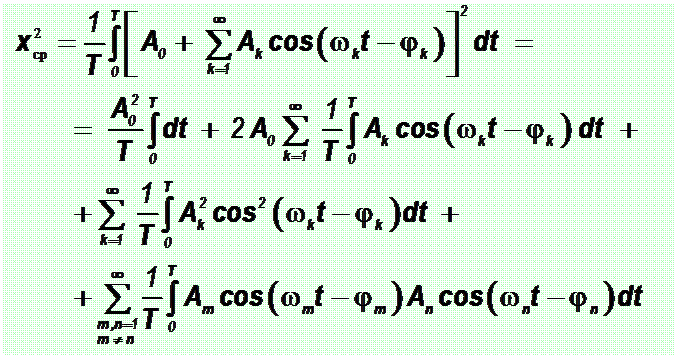 В правой части равенства второе слагаемое равно нулю как сумма средних значений гармонических сигналов, а четвёртое слагаемое - в силу ортогональности косинусоидальных функций в пределах периода.
В правой части равенства второе слагаемое равно нулю как сумма средних значений гармонических сигналов, а четвёртое слагаемое - в силу ортогональности косинусоидальных функций в пределах периода.
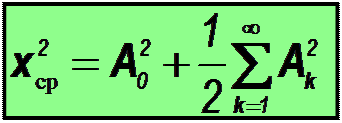 Отсюда среднее квадрата (средняя мощ-ность) периодического негармонического сигнала будет
Отсюда среднее квадрата (средняя мощ-ность) периодического негармонического сигнала будет
 2015-07-04
2015-07-04 359
359






