2015-07-04
616Мелкое замечание. Пусть x и h — независимые случайные величины с плотностям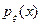и 
и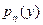 
. Плотность случайной величины x + h вычисляется по формуле свертки
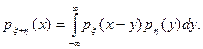
Равномерное распределение. Непрерывная случайная величина x имеет равномерное распределение на отрезке [a,b], если плотность распределения рx(x) сохраняет постоянное значение на этом промежутке:
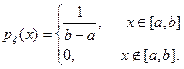
Функция распределения Fx(x) равномерно распределенной случайной величины равна
Fx(x)=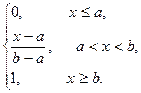 
Математическое ожидание и дисперсия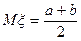 
; 
.
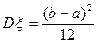Показательное (экспоненциальное) распределение. Непрерывная случайная величина x, принимающая неотрицательные значения, имеет показательное распределение с параметром l>0, если плотность распределения вероятностей случайной величины равна
рx(x)=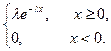 
Функция распределения показательного распределения имеет вид
Fx(x)=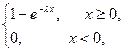 
а математическое ожидание и дисперсия равны М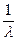x= 
, Dx=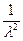 
.
Нормальное распределение (распределение Гаусса). Непрерывная случайная величина называется распределенной по нормальному закону с параметрам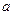и 
и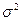 
, если ее плотность распределения равна
.
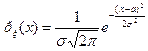Через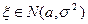 
обозначается множество всех случайных величин, распределенных по нормальному закону с параметрам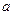и и .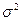
Функция распределения нормально распределенной случайной величины равна
.
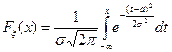Параметры нормального распределения суть математическое ожидание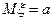 
и дисперсия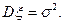 
В частном случае, когда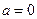 
и 
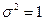нормальное распределение называется стандартным, и класс таких распределений обозначается 
.
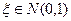В этом случае плотность стандартного распределения равна
,
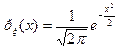а функция распределения
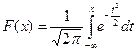
Такой интеграл не вычислим аналитически (не берется в «квадратурах»), и потому для функции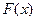 
составлены таблицы. Функция 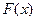связана с введенной в главе 4 функцией Лапласа
,
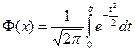следующим соотношением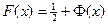 
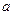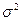. В случае же произвольных значений параметров и функция распределения 
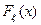случайной величины 
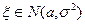связана с функцией Лапласа с помощью соотношения:
.
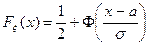Поэтому вероятность попадания нормально распределенной случайной величины 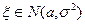на интервал 
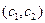можно вычислять по формуле
.
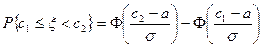Неотрицательная случайная величина x называется логарифмически нормально распределенной, если ее логарифм h=lnx подчинен нормальному закону. Математическое ожидание и дисперсия логарифмически нормально распределенной случайной величины равны М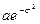x= 
и Dx=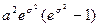 
.
Распределение Лапласа задается функцией p(x)=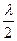 
e-lïxï, -¥<х<¥, (двусторонняя показательная плотность).
Дисперсия в два раза больше дисперсии случайной величины, распределенной по показательному закону Dx= =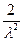 
.
Случайная величина x распределена по закону Вейбулла, если она имеет функцию плотности распределения, равную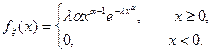 
Функция распределения в этом случае определяется следующим выражением:
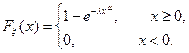
Распределению Вейбулла подчиняются времена безотказной работы многих технических устройств. В задачах данного профиля важной характеристикой является интенсивность отказа (коэффициент смертности) l(t) исследуемых элементов возраста t, определяемый соотношением l(t)=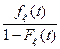 
. Если a=1, то распределение Вейбулла превращается в экспоненциальное распределение, а если a=2 - в так называемое распределение Рэлея.
Математическое ожидание распределения Вейбулла: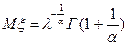 
и дисперсия - 
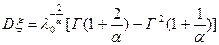, где Г(а) -функция Эйлера..
В различных задачах прикладной статистики часто встречаются так называемые «усеченные» распределения. Например, налоговые органы интересуются распределением доходов тех лиц, годовой доход которых превосходит некоторый порог с0, установленный законами о налогообложении. Эти распределения оказываются приближенно совпадающими с распределением Парето. Распределение Парето задается функциями
Fx(x)=P(x<x)=1–(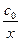
)a;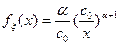 
,
где a>0, а х>с0. Основные числовые характеристики этого распределения существуют не всегда, а лишь при соблюдении определенных требований к значению параметра a: математическое ожидание - Мx=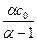 
при a>1, дисперсия - Dx= 
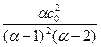существует при a>2;
