2015-07-04
1434
Рассмотрим балансный ФД. Такой детектор состоит из двух встречно включенных амплитудных детекторов, нагрузкой являются соответственно резисторы и конденсаторы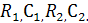 
При этом 
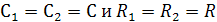. Одно из входных напряжений подводится к схеме с помощью
трансформатора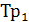 
со средней точкой таким образом, чтобы составляющие этого напряжения 
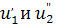имели одинаковую амплитуду и действовали на диоды 
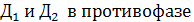то есть 
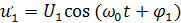и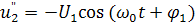 
.Второе входное напряжение 
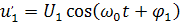через трансформатор 
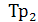подводится к диодам с одной фазой. Таким образом, на каждом из диодов действует сумма двух напряжений конденсаторы 
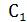и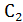 
для токов частот 
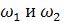представляют короткое замыкание: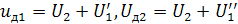 
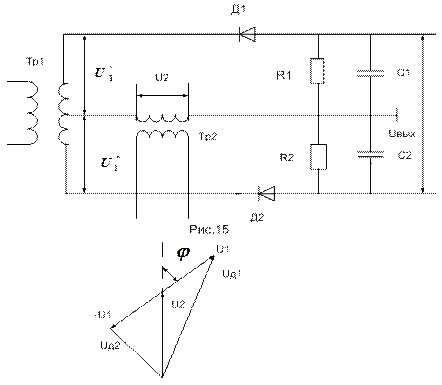
Рис.16
Амплитуды результирующих напряжений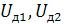 
можно определить графически с помощью векторных диаграмм рисунок (16).
Результирующий фазовый угол φ между векторами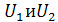 
определяются равенством φ=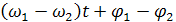 
С помощью диаграмм можно получить значение результирующих амплитуд напряжений, приложенных к диодам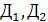 
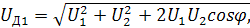(8);
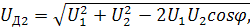(9);
Напряжение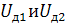 
детектируется на нагрузках амплитудных детекторов возникнут напряжения 
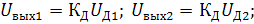где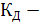 
коэффициент передачи амплитудного детектора.
Результирующее выходное напряжение фазового детектора:
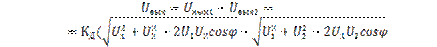
Это выражение представляет собой уравнение импульсно-фазовой характеристики балансного фазового детектора. Крутизну характеристики балансного фазового детектора можно найти, дифференцируя уравнение его импульсно-фазовой характеристики:
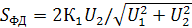(10);
Уравнение можно упростить, разложив каждое слагаемое в степенной ряд и ограничившись первыми членами разложения:
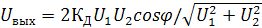(11);
При этом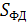 
по-прежнему определяется выражением (10). Если амплитуда одного из входных напряжений существенно больше амплитуды другого (например 
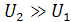) уравнение характеристики оказывается еще более простым: 
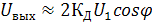(12);
При этом
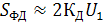(13);
Основное уравнение импульсно-фазовой характеристики (9) является симметричным относительно амплитуд входных сигналов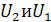 
.Поэтому с точки зрения работы схемы безразлично какой из входных сигналов будет являться опорным.
Для балансного фазового детектора характерно, что его входное напряжение зависит от соотношения амплитуд входных напряжений:(см.рис)
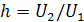(14);
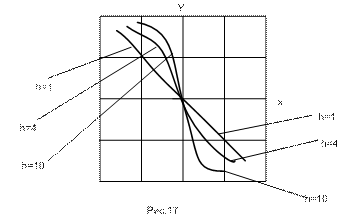
Амплитудно-фазовые характеристик, приведенные на данном рисунке построены по формуле(11) для различных значений h. По оси ординат отложим обобщенные значения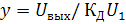 
. Анализ приведенных графиков позволит сделать следующие выводы. При 
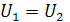характеристика практически считается линейной, крутизна ее согласно (10) будет равна:
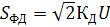(15);
Если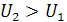 
то характеристика приближается косинусоидальной, а крутизна детектора стремится к своему максимально возможному значению(13).
Предельное значение обобщенной величины y=2 свидетельствует о том, что максимальное напряжение на выходе детектора не может превышать удвоенной величины наименьшего из входных напряжений (при условии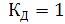 
). Предельное значение коэффициента передачи напряжения будет равно
.
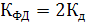При выполнении неравенства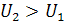 
величина максимального значения
выходного напряжения зависит практически только от наименьшего из входных напряжений, в данном случае от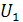 
. Следовательно, если требуется, чтобы 
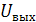оставалось неизменным при работе фазового детектора в условиях изменения амплитуды одного сигналов, необходимо обеспечить постоянство амплитуды наименьшего из двух входных напряжений. Например, при постоянной амплитуде опорного напряжения (
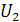) для сохранения неизменным входного напряжения пи колебаниях амплитуды напряжения входного сигнала (
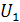) необходимо, чтобы всегда выполнялось условие 
.
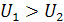Оценим приближенно порядок входных сопротивлений балансного фазового детектора. Если внутреннее сопротивление диода, намного меньше сопротивления нагрузки, то входное сопротивление последовательного диодного детектора при достаточно больших входных напряжениях приближенно равно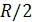 
.
Следовательно, входное сопротивление балансного фазового детектора с стороны первого входа, пересчитанное по вторичной обмотке трансформатора 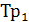(рис.15), будет равно сумме двух входных сопротивлений амплитудных диодных детекторов, то есть:
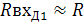(16);
Со стороны второго входа входное сопротивление, приведенное ко вторичной обмотке трансформатора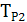 
, будет складываться на двух параллельно включенных входных сопротивлений диодных детекторов, следовательно:
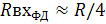(17);
Заметим, что для упрощения все входные напряжения и сопротивления в схеме рассматривались проведенными ко вторичным обмоткам трансформаторов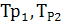 
. Очевидно эти величины можно легко пересчитать к первичным обмоткам, то есть непосредственно на оба входа схемы фазового детектора.
Рассмотрим некоторые соотношения между элементами нагрузки балансного фазового детектора. Как уже отмечалось, величину резистора R выбирают на условии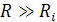 
. Постоянная времени нагрузки RC должна быть, с одной стороны такой, чтобы выполнялось известное из теории амплитудных детекторов неравенство:
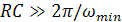(18);
где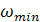 
-минимальная частота входных напряжений детектора. С другой стороны, чтобы при 
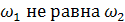не искажалось форма выходного напряжения и таким образом и таким образом обеспечивалась требуемое быстродействие, должно выполнятся условие
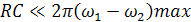(19);
Последнее неравенство, очевидно, теряет свой смысл, когда ω1 = ω2. В этом случае верхняя граница постоянной времени RC будет определяться возможной максимальной скоростью изменения фазового угла ω0 = ω1 – ω2 между сравниваемыми напряжениями.
