Пример распределенного риска

Ранее рассмотрен альтернативный вариант, когда страховой случай либо наступает с вероятностью р, и тогда выплачивается вся страховая сумма, либо случай не наступил, тогда выплаты нет.

Представляет интерес ситуация, где при наступлении страхового случая величина ущерба является случайной величиной с некоторым законом распределения. Рассмотрим дискретную величину.

Пример 6. Вероятность страхового случая р =0.1. Условное распределение:

Определить размер единовременной рисковой премии.

Сначала найдем условное математическое ожидание ущерба X (взвешенную среднюю): М(Х / А)=100·0.4+200·0.3+300·0.2+400·0.1=200;

Теперь: М(Х)=М(Х / А)· р +0· q =200·0.1+0·0.9=20. Это и будет искомой рисковой премией.

Пример 7. Рассмотрим непрерывно распределенный размер ущерба. Пусть случай наступает с вероятностью 0.05, и тогда ущерб распределен равномерно на отрезке (0, 600). Здесь условное математическое ожидание равно 300, тогда рисковая премия равна 15.

Разумеется, и для таких договоров представляет интерес задачи определения возможного отклонения фактического значения от ожидаемого, особенно, для всего портфеля. Именно на основании этого определяется надбавка, капитал, перестраховочная программа.

Пример 8. Объект застрахован от пожара на сумму 6 млн. Вероятность пожара 0.0001, а величина ущерба распределена равномерно от 0 до 6 млн. Найти среднее значение и дисперсию иска.

Из свойств равномерного распределения следует, что условные значения этих величин (при условии, что случился пожар) равны: М(Х / А)= S /2=3·10⁶, D(X / A)= S ²/12=3·10¹².

Тогда, учитывая вероятность, получим безусловные значения: М(Х)=300, D(X)=D(X / A)· p +M(X / A)²· pq =3·10⁸+(3·10⁶)²·0.0001·0.9999=(3+9)·10⁸=12·10⁸. Тогда СКО=3.46·10⁴; коэффициент вариации: 34600/300=115.

Здесь проиллюстрирована опасность для страховщика принятия одного риска.

Пример 9. Ущерб при пожаре (если он произошел) распределен по экспо­ненциальному закону со средним значением 2000. Предел ответственности страховой компании 5000. Найти среднее значение действительно предъявленного иска.

Уточним, если X < L, то компания платит X; иначе платит L, т.е. Y =min(X, L). Поэтому строим распределение величины действительно предъявляемого иска:

P(Y < х)=1, если х > L; или P(Y < x)=Р(Х < х), если х < L. Можно рассмотреть: P(Y > х)=0, если х > L; или P(Y < x)=P(Y > х), если х > L.

Теперь находим математическое ожидание, рассматривая вместо интеграла от 0 до бесконечности интеграл от 0 до L, (после L подынтегральная функция равна 0). Получим:

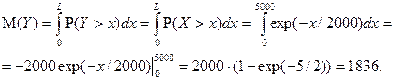
Отметим, что найденное среднее значение меньше параметра, и это будет иметь место при любом L, причем с увеличением L разность будет стремиться к 0. Это определяется свойствами экспоненциального распределения.