Темы: Векторная алгебра. Аналитическая геометрия.
Темы: 1). Координаты вектора, его длина. Деление отрезка пополам. Расстояние между точками. Проекция вектора на вектор. Скалярное произведение. Угол между векторами (косинус). Векторное произведение. Площадь треугольника и параллелограмма, объём пирамиды. 2). Длина вектора. Угол между векторами (синус). Векторное произведение, его модуль. Принадлежность четырёх точек одной плоскости. Площадь треугольника и параллелограмма, объём тетраэдра. 3). Компланарность, коллинеарность, ортогональность, равенство векторов. 4). Нахождение координат вектора по заданным условиям (коллинеарности, ортогональности). Скалярное, векторное, смешанное произведения и их приложения. 5). Прямая на плоскости (различные формы записи уравнения прямой на плоскости: проходящей через точку перпендикулярно вектору, параллельно вектору, через две точки, с угловым коэффициентом, в отрезках; угол между прямыми; точка пересечения прямых; расстояние от точки до прямой на плоскости; условия 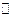 и
и 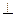 прямых). 6). Плоскость и прямая в пространстве (различные формы записи уравнения плоскости: проходящей через точку перпендикулярно вектору, через три точки, в отрезках; угол между плоскостями; расстояние от точки до плоскости; условия
прямых). 6). Плоскость и прямая в пространстве (различные формы записи уравнения плоскости: проходящей через точку перпендикулярно вектору, через три точки, в отрезках; угол между плоскостями; расстояние от точки до плоскости; условия 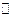 и
и 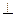 плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия
плоскостей; различные формы записи уравнения прямой в пространстве: проходящей через две точки, параметрическое; угол между прямыми, прямой и плоскостью; условия 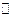 и
и 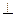 прямой и плоскости; точка пересечения прямой и плоскости). 7). Классификация кривых второго порядка. Нахождение вершины параболы, центра и радиуса окружности, центров эллипса и гиперболы. Канонические уравнения эллипса, гиперболы и параболы нахождение их фокусов и эксцентриситетов. Сфера: каноническое и нормальное уравнения, центр и радиус.
прямой и плоскости; точка пересечения прямой и плоскости). 7). Классификация кривых второго порядка. Нахождение вершины параболы, центра и радиуса окружности, центров эллипса и гиперболы. Канонические уравнения эллипса, гиперболы и параболы нахождение их фокусов и эксцентриситетов. Сфера: каноническое и нормальное уравнения, центр и радиус.
ВАРИАНТ №0
| № | Задания | Ответы |
Если в треугольнике 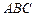 : : 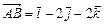 и и 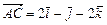 , то , то  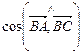 равен…
1) равен…
1) 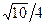 2) 2) 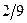 3) 3) 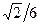 4) 4) 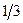 5) 5) 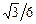
| 3) 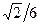
| |
Векторы 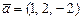 , , 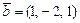 и и 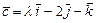 компланарны, если значение параметра компланарны, если значение параметра 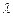 равно… равно…
| 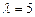
| |
1) 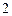 2) 2) 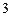 3) 3) 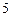 4) 4) 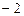 5) 5) 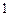
| ||
Две противоположные вершины квадрата 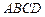 находятся в точках находятся в точках 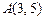 , , 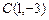 . Тогда его площадь . Тогда его площадь 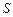 равна… Записать ответ. равна… Записать ответ.
| 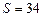
| |
Площадь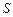 параллелограмма, построенного на векторах параллелограмма, построенного на векторах 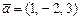 и и 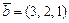 равна:
1) равна:
1) 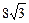 2) 2) 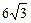 3) 3) 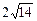 4) 4) 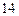 5) 5) 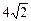
| 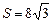
| |
Известно, что: 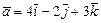 , , 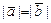 , , 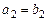 , , 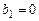 , , 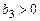 . Тогда вектор . Тогда вектор 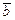 имеет координаты имеет координаты 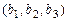 , где , где 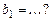 , , 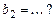 , , 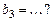 Ответ записать в виде: Ответ записать в виде: 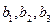
| 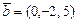
| |
Плоскости 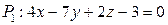 и и 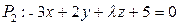 будут взаимно перпендикулярны, если параметр будут взаимно перпендикулярны, если параметр 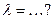 Записать ответ. Записать ответ.
| 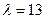
| |
Даны плоскости: а) 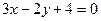 ; б) ; б) 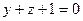 ; в) ; в) 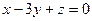 .
Из них оси .
Из них оси 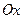 параллельны только… параллельны только…
| 3) | |
| 1) толькоа) 2) ни одна 3) только б) 4) толькоа)ив) 5) тольков) 6) все | ||
Векторы 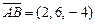 и и 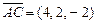 совпадают со сторонами треугольника совпадают со сторонами треугольника 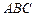 . Тогда вектор . Тогда вектор 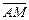 , совпадающий с медианой треугольника , совпадающий с медианой треугольника 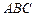 , имеет координаты , имеет координаты 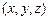 , где , где 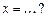 , , 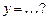 , , 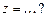 Ответ записать в виде: Ответ записать в виде: 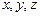
| 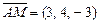
| |
Вектор 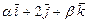 коллинеарен вектору коллинеарен вектору 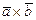 , где , где 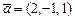 , , 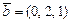 при значениях параметров при значениях параметров 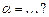 , , 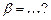 Ответ записать в виде: Ответ записать в виде: 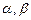
| 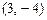
| |
Известно, что фокусы гиперболы совпадают с фокусами эллипса 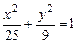 и её эксцентриситет и её эксцентриситет 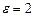 .Тогдаканоническое уравнение гиперболы имеет вид: .Тогдаканоническое уравнение гиперболы имеет вид: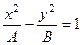 ,где ,где 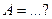 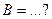 ( (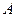 , , 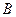 - целые числа). Ответ записать в виде: - целые числа). Ответ записать в виде: 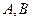
| 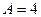 , ,
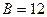 , ,
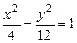
|
 2015-07-04
2015-07-04 536
536







