def 1 Уравнение вида
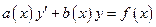 , (1)
, (1)
где 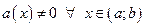 , называется линейным дифференциальным уравнением I порядка (ЛДУ).
, называется линейным дифференциальным уравнением I порядка (ЛДУ).
def 2 Если в ЛДУ (1) 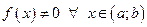 , то его называют неоднородным (ЛНДУ).
, то его называют неоднородным (ЛНДУ).
def 3 Если в ЛДУ (1) 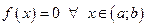 , то его называют однородным (ЛОДУ).
, то его называют однородным (ЛОДУ).
Замечание 1 Далее будем считать, что функции 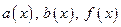 являются непрерывными
являются непрерывными 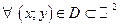 , где D – область интегрирования ЛДУ (1), в которой выполнены все условия теоремы существования и единственности решения.
, где D – область интегрирования ЛДУ (1), в которой выполнены все условия теоремы существования и единственности решения.
Th 1 Пусть функции 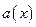 и
и 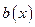 непрерывны
непрерывны 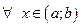 . Тогда общее решение ЛОДУ (1)
. Тогда общее решение ЛОДУ (1) 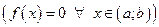 может быть найдено по формуле:
может быть найдено по формуле:
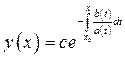 , (2)
, (2)
где с – произвольная константа. Частное решение ЛОДУ, удовлетворяющее начальному условию 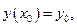 может быть найдено по формуле:
может быть найдено по формуле:
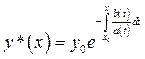 . (3)
. (3)
Способы решения ЛНДУ.
1) Метод вариации произвольной постоянной (метод Лагранжа).
Данный подход базируется на следующей теореме.
Th 2 Пусть функции 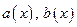 и
и 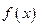 непрерывны
непрерывны 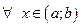 . Тогда общее решение ЛНДУ (1)
. Тогда общее решение ЛНДУ (1) 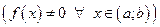 может быть найдено по формуле:
может быть найдено по формуле:
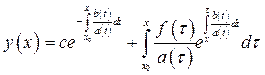 , (4)
, (4)
где с – произвольная константа. Частное решение ЛНДУ, удовлетворяющее начальному условию 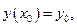 может быть найдено по формуле:
может быть найдено по формуле:
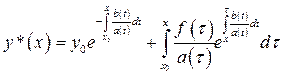 . (5)
. (5)
Замечание 2 Формула (4) показывает, что общее решение ЛНДУ равно сумме общего решение ЛОДУ, соответствующего данному ЛНДУ и частному решению этого ЛНДУ, то есть:
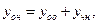 (6)
(6)
где 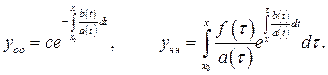 (7)
(7)
В связи с громоздкостью, формулы (2) и (3) не запоминают, они легко могут быть получены при решении ЛОДУ, как ДУ с разделяющимися переменными. Также не имеет смысла помнить формулы (4)-(7), которые также легко могут быть получены в результате реализации алгоритма решения ЛНДУ (1).
Укажем общий алгоритм решения ЛНДУ вида (1) методом вариации произвольной постоянной:
1) Составить для ЛНДУ (1) соответствующее ему ЛОДУ:
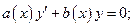 (8)
(8)
2) Проинтегрировать полученное уравнение (8) как ДУ с разделяющимися переменными, это приведёт к уравнению (2);
3) Полагая в уравнении (2) 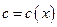 , выполнить подстановку правой части равенства (2) в ЛНДУ (1), учитывая, что:
, выполнить подстановку правой части равенства (2) в ЛНДУ (1), учитывая, что:
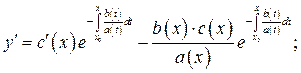
4) Проинтегрировать полученное таким образом ДУ с разделяющимися переменными для функции 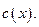
5) Подставить найденную функцию 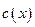 в формулу (2).
в формулу (2).
6) Записать ответ.
Пример 1 Решить задачу Коши 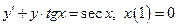 (9) методом вариации произвольной постоянной.
(9) методом вариации произвольной постоянной.
Решение: Покажем, что ДУ (9) интегрируется по выше указанной схеме.
Составим и найдём общее решение для ЛОДУ, соответствующее ЛНДУ (9):
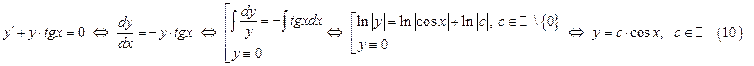
Уравнение (10) представляет собой общий интеграл ЛОДУ, соответствующего ЛНДУ (9). Полагаем в формуле (10) 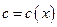 . Теперь выполним подстановку равенства (10) в ЛНДУ (9):
. Теперь выполним подстановку равенства (10) в ЛНДУ (9):
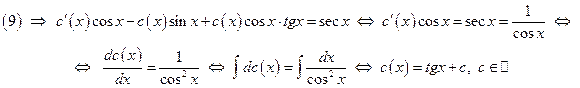
Таким образом, подставляя найденную функцию 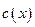 в уравнение (10), найдём общее решение ЛНДУ (9):
в уравнение (10), найдём общее решение ЛНДУ (9):
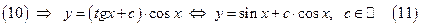
Подставим начальные условия в равенство (11):
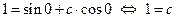
Значит, интегральная кривая удовлетворяющая задаче Коши (9) имеет вид:
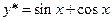
Ответ: 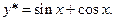
2) Метод Бернулли.
Алгоритм данного подхода:
1) В ЛНДУ (1) выполняют замену:
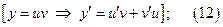
2) В полученном таким образом ДУ выделить в скобках левую часть ЛОДУ (8) для функции 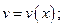
3) Перейти к системе вида:
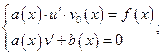 (13)
(13)
4) Из второго уравнения системы (13) найти функцию 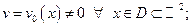
5) Подставить функцию 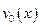 в первое уравнение системы (13), а затем проинтегрировать это ДУ как ДУ с разделяющимися переменными. Так будет найдено общее решение этого ДУ:
в первое уравнение системы (13), а затем проинтегрировать это ДУ как ДУ с разделяющимися переменными. Так будет найдено общее решение этого ДУ:
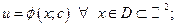
6) Найти общее решение ЛНДУ (1):
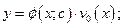
7) Записать ответ.
Пример 2 Решить задачу Коши 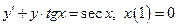 (9) методом Бернулли.
(9) методом Бернулли.
Решение: Выполним в ДУ (9) замену Бернулли (12) и проинтегрируем полученное ДУ:
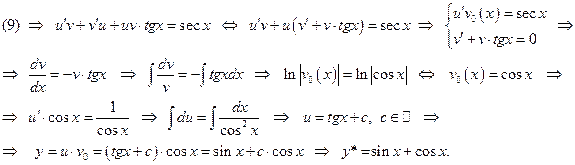
Ответ: 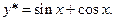
Дифференциальное уравнение Бернулли.
Определение 4 Уравнение вида
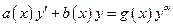 , (14)
, (14)
где 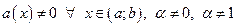 называется дифференциальным уравнением Бернулли (ДУ Бернулли) с показателем α.
называется дифференциальным уравнением Бернулли (ДУ Бернулли) с показателем α.
Замечание 3 При 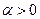 ДУ Бернулли (14), всегда имеет решение
ДУ Бернулли (14), всегда имеет решение 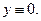
Чтобы решить ДУ Бернулли (14) можно выполнить замену:
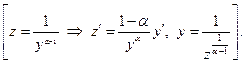 (15)
(15)
Эта подстановка приведёт уравнение (14) к ЛНДУ вида (1) для функции 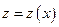 , однако при этом всегда будет потеряно решение
, однако при этом всегда будет потеряно решение 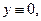 если
если 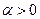 . Хотя, для того чтобы решить ДУ Бернулли (14), нет необходимости в выполнении замены (15). ДУ (14) может быть проинтегрировано как с использованием метода вариации произвольной постоянной, так и с помощью замены Бернулли (12).
. Хотя, для того чтобы решить ДУ Бернулли (14), нет необходимости в выполнении замены (15). ДУ (14) может быть проинтегрировано как с использованием метода вариации произвольной постоянной, так и с помощью замены Бернулли (12).
Замечание 4 Иногда встречается запись ДУ, в котором роли переменных изменены: за х принимают неизвестную функцию, а за у независимую переменную. Поэтому иногда, некоторые ДУ становятся линейными или ДУ Бернулли, если полагать, что оно для функции 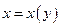 .
.
Напомним, что:
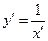
Пример 3 Решить ДУ 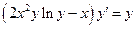 . (16)
. (16)
Решение: Область существования и интегрирования данного ДУ задаётся выражением 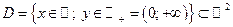 .Покажем, что (16) является ДУ Бернулли относительно функции
.Покажем, что (16) является ДУ Бернулли относительно функции 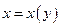 :
:
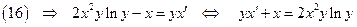 (17)
(17)
Значит, (17) представляет собой ДУ Бернулли для функции 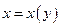 с показателем
с показателем 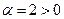 , следовательно, ДУ (17) всегда имеет решение
, следовательно, ДУ (17) всегда имеет решение 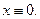 Однако, функция
Однако, функция 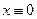 не является решением исходного уравнения (16).
не является решением исходного уравнения (16).
Решим уравнение (17) двумя способами:
1) Метод вариации произвольной постоянной:
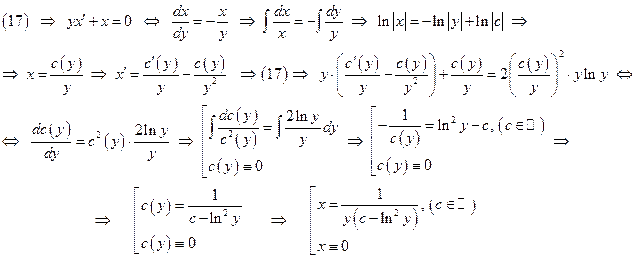
2) Метод Бернулли:
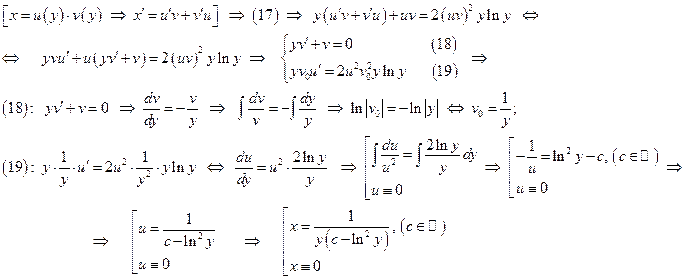
Ответ: 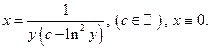
 2015-07-04
2015-07-04 2352
2352