Пусть вероятности p и q – фиксированы, а k изменяется от 0 до n, тогда вероятность pn (k) – это функция k. Найдем такое число k 0, которое максимизирует функцию pn (k). Это число естественно назвать наивероятнейшим числом появления события А (наивероятнейшим числом появления “успеха”). Сравним два числа - pn (k) и pn (k+ 1).
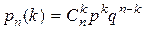 ;
; 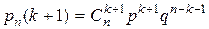 .
.
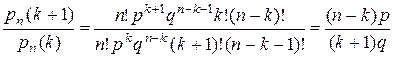 . (6.3)
. (6.3)
Отношение (6.3) больше 1, если (n - k) p > (k+ 1) q. Тогда np - q > > k (p+q) =k.
Итак, пока 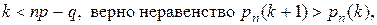 т.е. вероятности pn (k) монотонно возрастают. Соответственно, когда k > np - q, то верно неравенство pn (k+ 1) < pn (k) и вероятности pn (k) начинают монотонно убывать. Если число np – q целое, то имеем два наивероятнейших числа:
т.е. вероятности pn (k) монотонно возрастают. Соответственно, когда k > np - q, то верно неравенство pn (k+ 1) < pn (k) и вероятности pn (k) начинают монотонно убывать. Если число np – q целое, то имеем два наивероятнейших числа: 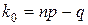 и
и 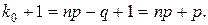
Если же число np – q дробное, то наивероятнейшее число k 0одно: k 0– это наименьшее целое число, превосходящее np – q. Другими словами, 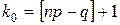 , где символ [ а ] означает целую часть числа а (рис.6.1).
, где символ [ а ] означает целую часть числа а (рис.6.1).
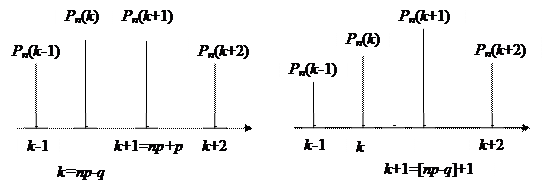
Рис.6.1
Поясним рис. 6.1
Левая диаграмма на рис. 6.1 Правая диаграмма на рис. 6.1
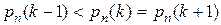 ;
; 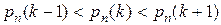 ;
;
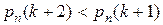 ;
; 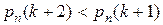 ;
;
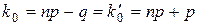 .
. 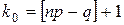 .
.
 2015-07-04
2015-07-04 357
357








