Наличие взаимосвязи между двумя показателями устанавливается с помощью корреляционного анализа по величине коэффициента корреляции Пирсона (форм. 6) - 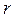 .
.
При 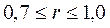 динамический ряд показателя имеет устойчивую сильную взаимосвязь с другим показателем. При
динамический ряд показателя имеет устойчивую сильную взаимосвязь с другим показателем. При 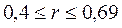 говорят о наличии средней взаимосвязи. Величина коэффициента корреляции в пределах
говорят о наличии средней взаимосвязи. Величина коэффициента корреляции в пределах 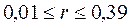 свидетельствует об отсутствии или очень слабой взаимосвязи. Отрицательные значения коэффициента корреляции указывают на наличие обратной взаимосвязи.
свидетельствует об отсутствии или очень слабой взаимосвязи. Отрицательные значения коэффициента корреляции указывают на наличие обратной взаимосвязи.
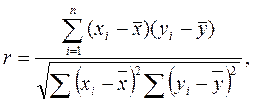 (6)
(6)
где 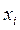 - показатель фактора или времени.
- показатель фактора или времени.
С целью подтверждения взаимосвязи коэффициент корреляции необходимо проверить на статистическую значимость по 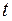 - критерию Стьюдента (форм. 7) –
- критерию Стьюдента (форм. 7) – 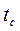 :
:
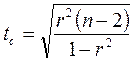 (7)
(7)
Полученные значения 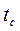 сравнивают с табличным значением
сравнивают с табличным значением 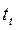 – критерия для 5% уровня значимости. Если расчетное значение tc больше tt, это свидетельствует о статистической значимости
– критерия для 5% уровня значимости. Если расчетное значение tc больше tt, это свидетельствует о статистической значимости 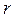 .
.
3. Построение регрессионных моделей (форм. 8–20)
Регрессионный анализ позволяет построить математическую модель показателя в зависимости от влияющего фактора или от времени (тренд).
Регрессионное моделирование целесообразно проводить на основе аналитического выравнивания с использованием тринадцати наиболее распространенных аппроксимирующих функций (форм. 8-20):
1) линейная 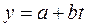 (8)
(8)
2) экспоненциальная 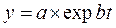 (9)
(9)
3) степенная 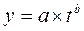 (10)
(10)
4) гиперболическая первого типа 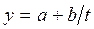 (11)
(11)
5) гиперболическая второго типа 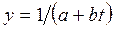 (12)
(12)
6) гиперболическая третьего типа 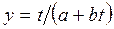 (13)
(13)
7) логарифмическая 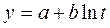 (14)
(14)
8) S-образная 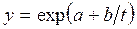 (15)
(15)
9) обратнологарифмическая 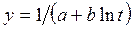 (16)
(16)
10) модифицированная экспонента 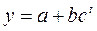 (17)
(17)
11) кривая Гомпертца 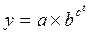 (18)
(18)
12) логистическая 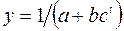 (19)
(19)
13) параболическая 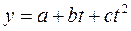 (20)
(20)
где 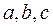 – параметры моделей,
– параметры моделей, 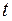 – время (годы).
– время (годы).
Если в модели в качестве влияющего аргумента вводятся другие показатели, то они обозначаются символом 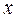 . При этом модели 8–20 имеют аналогичный вид, только
. При этом модели 8–20 имеют аналогичный вид, только 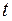 заменяется на
заменяется на 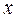 . Например, линейная функция примет вид
. Например, линейная функция примет вид 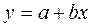 и т.д.
и т.д.
4. Выбор оптимальной модели (форм. 21–23)
Для использования регрессионных моделей с целью разработки прогноза изучаемого показателя необходимо выбрать оптимальные модели, то есть модели, наиболее точно описывающие исследуемое явление. Процесс выбора осуществляется с помощью специальных критериев оптимальности. Для их расчета необходимо предварительно по всем моделям вычислить теоретические ретроспективные значения показателя, затем на основе полученного информационного массива выбрать оптимальные модели, которые отвечают критериям оптимальности. В число таких критериев входят:
1) коэффициент корреляции Пирсона – 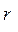 (форм. 6), рассчитанный между фактическими и теоретическими значениями показателя, найденными по регрессионной модели;
(форм. 6), рассчитанный между фактическими и теоретическими значениями показателя, найденными по регрессионной модели;
2) коэффициент детерминации – 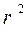 , измеряется в процентах и свидетельствует о доле дисперсии, объясняющейся регрессией по данной модели;
, измеряется в процентах и свидетельствует о доле дисперсии, объясняющейся регрессией по данной модели;
3) средняя абсолютная процентная ошибка 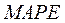 (Mean Absolute Percentage Error) (форм. 21):
(Mean Absolute Percentage Error) (форм. 21):
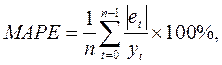 (21)
(21)
где 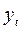 – фактическое значение показателя,че
– фактическое значение показателя,че
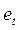 – ошибка прогноза (форм. 22):
– ошибка прогноза (форм. 22):
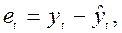 (22)
(22)
где 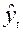 – теоретическое ретроспективное значение, рассчитанное по данной регрессионной модели.
– теоретическое ретроспективное значение, рассчитанное по данной регрессионной модели.
Если значение 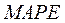 меньше 10%, то это указывает на высокую точность подбора аппроксимирующей функции и оптимальность модели;
меньше 10%, то это указывает на высокую точность подбора аппроксимирующей функции и оптимальность модели;
4) средняя процентная ошибка 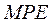 (Mean Percentage Error)
(Mean Percentage Error)
(форм. 23):
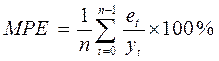 (23)
(23)
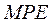 является показателем смещенности прогноза, ее величина не должна превышать 5%.
является показателем смещенности прогноза, ее величина не должна превышать 5%.
Вышеприведенные критерии являются методами верификации прогнозов, направленных на оценку достоверности и точности прогнозов.
5. Прогнозирование (форм. 24-25)
Прогнозирование осуществляется по выбранной оптимальной регрессионной модели. Если модель является факторной, то в нее вводится прогнозное значение аргумента.
После расчета прогноза необходимо найти стандартную ошибку прогноза – 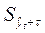 (форм. 24):
(форм. 24):
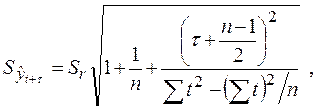 (24)
(24)
где 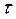 – период упреждения прогноза;
– период упреждения прогноза;
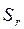 – стандартная ошибка уравнения (форм. 25):
– стандартная ошибка уравнения (форм. 25):
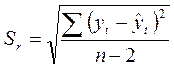 (25)
(25)
Затем рассчитываются доверительные интервалы прогноза в пределах
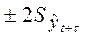
 2015-07-04
2015-07-04 413
413








