Преобразование нелинейной цепью суммы двух гармонических колебаний

Свойство нелинейной цепи обогащать спектр входного сигнала наиболее ярко проявляется при воздействие на нее суммы нескольких гармонических колебаний с различными частотами. Рассмотрим простейший случай, когда вольт-амперная характеристика нелинейного элемента в окрестностях рабочей точки описывается полиномом второй степени:

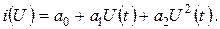(6. 14)

На вход этого элемента полается бигармоническое колебание вида

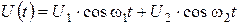. (6. 15)

Ток через нелинейный элемент определим, подставляя (6. 15) в (6. 14):

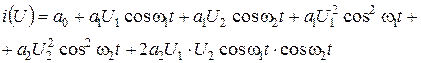
Использую тригонометрические формулы:

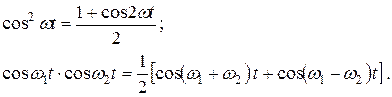
получим значения тока в следующим виде: 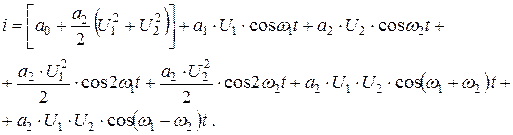(6. 16)

Спектральная диаграмма тока в соответствие с (6. 16) показана на рисунке 6.10.

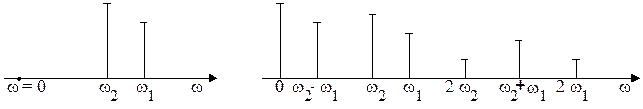
Рисунок 6. 10

Принципиально новым результатом по сравнению с воздействием на нелинейный элемент одного гармонического колебания является появление спектральных составляющих с частотам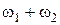и и 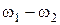, которые называются комбинационными частотами.

В более общем случае ВАХ нелинейного элемента аппроксимируется полиномом n-ой степени в соответствие с выражением

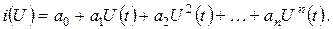(6. 17)

Подставляя значение бигармонического сигнала (6. 15) в (6. 7), получим:

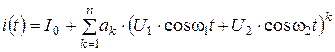(6. 18)

Чтобы найти спектральный состав тока в соответствии с (6. 18) надо для каждого значения 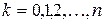составить развернутое выражение k-ой составляющей 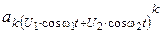, выразив его слагаемые через гармонические функции. Расчеты показывают, что составляющие высших степеней приводят к появлению колебаний кратных частот 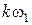и 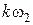, а также комбинационных частот вида

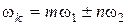
где m и n –– целые положительные числа, значения которых определяются видом ВАХ нелинейного элемента.

Эффект обогащения спектра нелинейным элементом при воздействие на него суммы гармонических колебаний лежит в основе работе многих радиотехнических устройств.