Режим большого сигнала

Амплитуда переменного напряжения настолько велика, что рабочий участок выходит за пределы линейного участка вольт-амперной характеристики. Форма тока отличается от косинусоиды. В этих условиях пренебрегать членами высших степеней ряда (6.7) нельзя, так как эти высшие составляющие и будут определять тот эффект, который дает нелинейность. Продукты нелинейности количественно определяются членами полинома (6.7) при .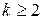

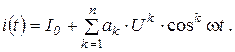
Составим таблицу составляющих ряда (6. 7) при различных k.

Таблица 6. 1

k		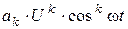Частота

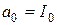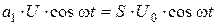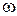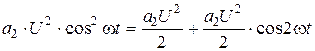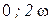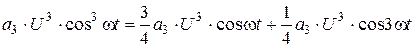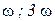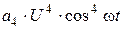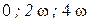Видно, что члены четных степеней ряда дают слагаемые четных гармоник, а члены нечетных степеней приводят к появлению составляющих всех нечетных гармоник. Из этого следует:

1. Нелинейность цепи приводит к тому, что спектр тока 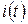в общем случае содержит постоянную составляющую 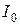и гармоники с частотами 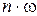, где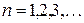

2. Соотношения между амплитудами отдельных гармоник зависят от характера нелинейности, положения исходной рабочей точки на характеристике, а также от амплитуды возбуждающего колебания.

6.4.2 Исследование нелинейной цепи методом кусочно-линейной аппроксимации

Метод применяется в тех случаях, когда вольт-амперную характеристику можно аппроксимировать с достаточной точностью двумя прямолинейными участками (рисунок 6. 8).

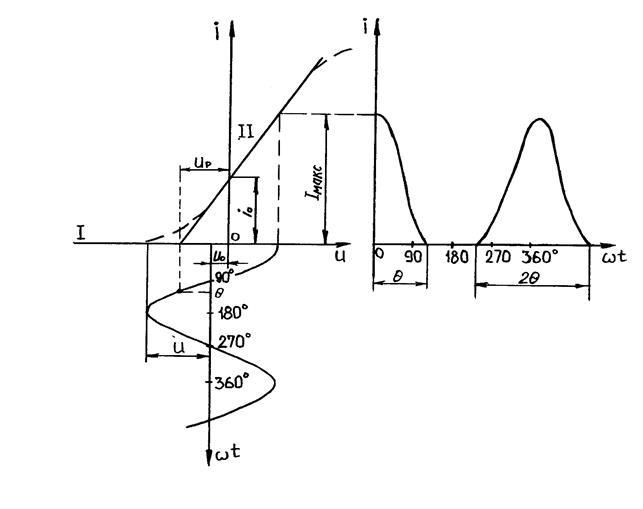
Рисунок 6. 8

Пусть имеется нелинейный элемент с известной вольт-амперной характеристикой и на него поданы напряжение смещения 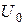и гармоническое косинусоидальное напряжение с амплитудой 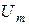(рисунок 6. 8. б). Ток в цепи с нелинейным элементом в этом случае имеет форму отдельных импульсов. Длительность импульсов можно выражать в электрических градусах через угол отсечки. Углом отсечки называется половина выраженной в градусах длительности импульсов тока. Угол отсечки может изменяться от 0 до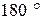

.

Определим аналитическое выражение тока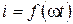

Уравнения участка II вольт-амперной характеристики:

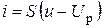(6. 8) Так как 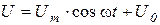, то подставив значение в (6. 8), получим

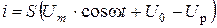(6. 9)

Из (6. 9) определим угол отсечки 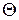. Согласно рисунку 6. 8 при 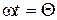ток , значит

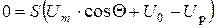(6. 10)

откуда

.

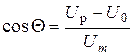Определим, как зависит текущее значение тока i от угла отсечки 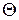. Для этого вычтем из (6. 9) соотношение (6. 10), получим

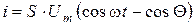. (6. 11)

Пронормируем значения 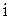относительно максимального значения тока I_МАКС. Максимальный ток протекает в цепи при 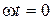. Тогда из выражения (6. 11) получим:

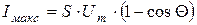. (6. 12)

Разделив (6. 11) на (6. 12), получим нормированное значение тока

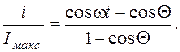(6. 13)

Это соотношение показывает, что для определения мгновенного значения нормированного тока достаточно знать угол отсечки . Используя выражения (6. 13), можно рассчитать постоянную составляющую и амплитуду всех гармоник тока: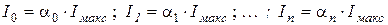

где 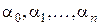–– нормированные коэффициенты Берга.

Коэффициент постоянной составляющей 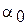определяется следующим образом (методика определения такая же, как и для определения коэффициентов в разложении Фурье):

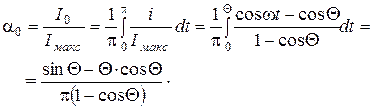
Коэффициент первой гармоники:

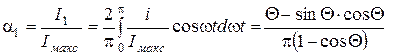
и т. д.

Видно, что все коэффициенты 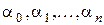зависят только от угла отсечки. Значения коэффициентов 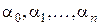в зависимости от рассчитаны, табулированы и представлены в справочниках в виде графиков (рисунок 6. 9).

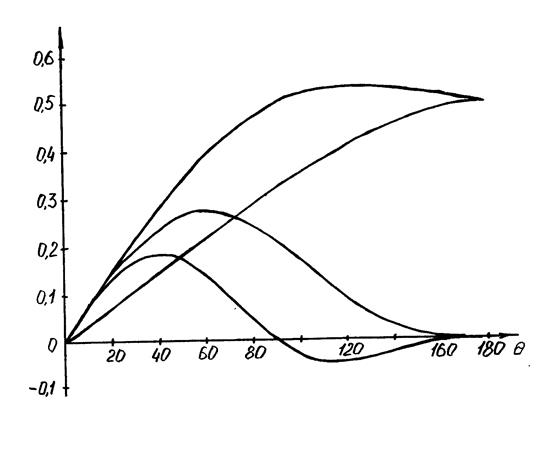
Рисунок 6. 9

Возможные режимы работы нелинейных элементов принято классифицировать по величине угла отсечки :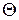

режим класса А: ;

режим класса В: ;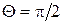

режим класса АВ: ;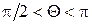

режим класса С: .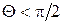

Метод кусочно-линейной аппроксимации позволяет выразить все величины, характеризующий режим цепи, через одну величину – угла осечки 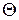, который и будет определять характер и величину образующихся гармонических составляющих.