Математическая статистика

1) Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х _i, а во второй строке – соответственные частоты n _i количественного признака Х). Требуется найти:

1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение;

2. Доверительные интервалы для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.

3. Пользуясь критерием Пирсона, при уровне значимости a=0,05, установить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с данными выборки объема n=100:

1.1)

хi
ni

1.2)

хi	10,6	15,6	20,6	25,6	30,6	35,6	40,6
ni

1.3)

хi
ni

1.4)

хi	12,4	16,4	20,4	24,4	28,4	32,4	36,4
ni

1.5)

хi
ni

1.6)

хi
ni

1.7)

хi	10,2	10,9	11,6	12,3		13,7	14,4
ni

1.8)

хi	11,5		12,5		13,5		14,5
ni

1.9)

хi
ni

1.10)

хi
ni

1.11)

хi	12,5		13,5		14,5		15,5
ni

1.12)

хi
ni

2. Найти по данной корреляционной таблице:

а) выборочное уравнение прямой 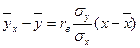регрессии Y на Х;

б) выборочное корреляционное отношение 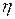_YX

2.1)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.2)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.3)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.4)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.5)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.6)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.7)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.8)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.9)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.10)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100