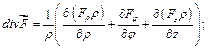Пусть 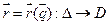 - биективное и непрерывно дифференцируемое отображение области
- биективное и непрерывно дифференцируемое отображение области 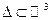 на область
на область 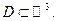 В координатном виде:
В координатном виде:
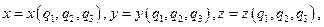
координаты 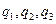 называются криволинейными координатами точек области
называются криволинейными координатами точек области 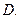 Поверхности
Поверхности 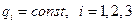 являются координатными. Координатные линии имеют вид:
являются координатными. Координатные линии имеют вид: 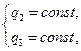 (линия изменения
(линия изменения 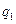 ),
), 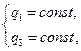 (линия изменения
(линия изменения 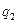 ),
), 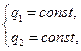 (линия изменения
(линия изменения 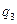 ).
).
Примеры: 1) цилиндрические координаты 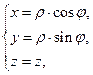
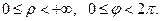
Поверхности 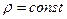 круговые цилиндры с осью
круговые цилиндры с осью 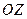 , поверхности
, поверхности 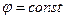 - полуплоскости, ограниченные осью
- полуплоскости, ограниченные осью 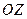 , плоскости
, плоскости 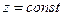 - горизонтальные плоскости. Координатные линии: изменения
- горизонтальные плоскости. Координатные линии: изменения 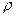 - горизонтальные лучи, выходящие из точек оси
- горизонтальные лучи, выходящие из точек оси 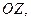 изменения
изменения 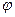 - горизонтальные окружности с центром на оси
- горизонтальные окружности с центром на оси 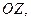 изменения
изменения 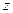 - вертикальные прямые.
- вертикальные прямые.
2) сферические координаты 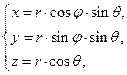
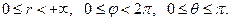
Координатные поверхности: 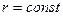 - сферы с центром в точке
- сферы с центром в точке 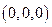 ,
, 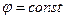 - полуплоскости, ограниченные осью
- полуплоскости, ограниченные осью 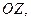
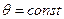 - круговые полуконусы с вершиной в начале координат и с осью
- круговые полуконусы с вершиной в начале координат и с осью 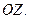 Координатные линии: изменения
Координатные линии: изменения 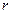 - лучи, выходящие изначала координат, изменения
- лучи, выходящие изначала координат, изменения 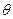 - полуокружности с центром в начале координат и с концами на оси
- полуокружности с центром в начале координат и с концами на оси 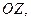 изменения
изменения 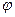 - горизонтальные окружности с центром на оси
- горизонтальные окружности с центром на оси 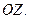
Обозначим: 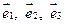 - единичные векторы касательных к координатным линиям
- единичные векторы касательных к координатным линиям 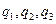 . Будем считать их ортогональными. Векторы
. Будем считать их ортогональными. Векторы 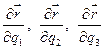 направлены по касательной к координатным линиям:
направлены по касательной к координатным линиям: 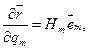 где
где 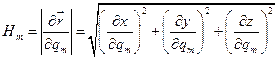 - коэффициенты Ламэ.
- коэффициенты Ламэ.
Примеры. 1) цилиндрические координаты: 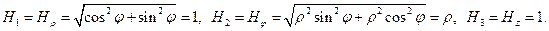
2) сферические координаты:
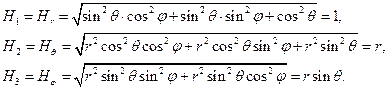
Возьмём координатную поверхность 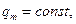 нормаль к ней направлена по
нормаль к ней направлена по 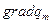 , а в силу ортогональности координат, направлена по касательной к линии
, а в силу ортогональности координат, направлена по касательной к линии 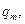 т.е. по
т.е. по 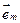 , следовательно:
, следовательно: 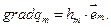 Покажем, что
Покажем, что 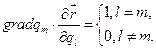 Действительно,
Действительно,
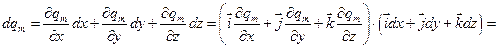
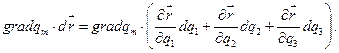
По линейной независимости 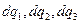 коэффициенты левой и правой частей полученного равенства при одинаковых дифференциалах совпадают, но в левой части отличен от нуля и равен 1 только коэффициент при
коэффициенты левой и правой частей полученного равенства при одинаковых дифференциалах совпадают, но в левой части отличен от нуля и равен 1 только коэффициент при 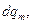 следовательно,
следовательно, 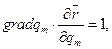 а остальные коэффициенты правой части есть нули. Тогда
а остальные коэффициенты правой части есть нули. Тогда
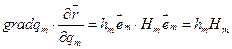
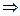
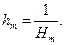
Таким образом, 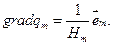
Рассмотрим элементарную ячейку, образованную тремя парами смежных координатных поверхностей, и обозначим 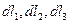 длины рёбер ячейки. Имеем:
длины рёбер ячейки. Имеем: 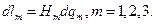 Действительно, с точностью до бесконечно малых порядка выше первого
Действительно, с точностью до бесконечно малых порядка выше первого 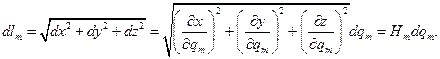
- Градиент
По определению градиента 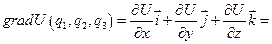
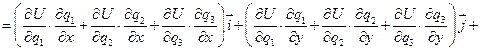
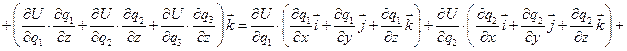
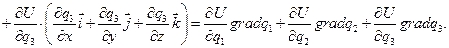
Используя (1), получим: 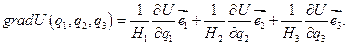 (2)
(2) 
Примеры. 1) цилиндрические координаты: 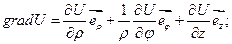
2) сферические координаты: 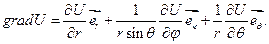
2. Дивергенция
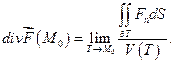
Рассмотрим параллелепипед – элементарную ячейку - 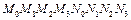 и подсчитаем поток поля
и подсчитаем поток поля 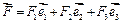 через грань
через грань 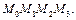 На ней
На ней 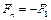 - нормаль направлена вне тела. Тогда
- нормаль направлена вне тела. Тогда 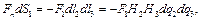 причём здесь
причём здесь 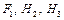 определяются на поверхности
определяются на поверхности 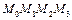 при
при 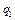 . Аналогично поток поля через грань
. Аналогично поток поля через грань 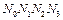 приближённо равен
приближённо равен 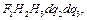 но здесь
но здесь 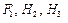 подсчитываются при
подсчитываются при 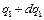 . Используя формулу Тейлора, получим:
. Используя формулу Тейлора, получим: 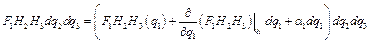 , где
, где 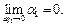 Тогда сумма потоков через противоположные грани параллелепипеда равна:
Тогда сумма потоков через противоположные грани параллелепипеда равна: 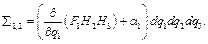 Определяя потоки через две другие пары противоположных граней и складывая их, найдём:
Определяя потоки через две другие пары противоположных граней и складывая их, найдём: 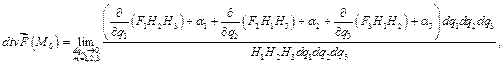 где
где 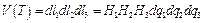 - с точностью до бесконечно малых более высокого порядка. Итак,
- с точностью до бесконечно малых более высокого порядка. Итак, 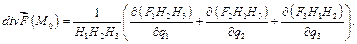
Примеры.
2) сферические координаты: 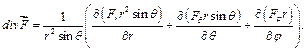
Ротор
Найдём проекции ротора на координатные линии: 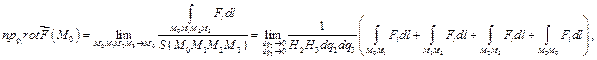 где
где 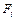 - проекция поля на направление касательной к кривой интегрирования. На
- проекция поля на направление касательной к кривой интегрирования. На 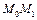
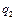 изменяется от
изменяется от 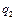 до
до 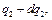
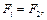
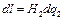 и
и 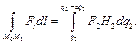 На
На 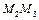
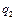 изменяется от
изменяется от 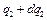 до
до 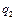 ,
, 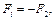
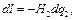 при этом
при этом 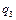 имеет значение
имеет значение 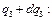
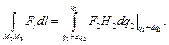 Формула Тейлора приводит к следующему результату:
Формула Тейлора приводит к следующему результату: 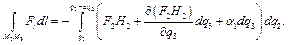 Тогда, используя теорему о среднем, будем иметь:
Тогда, используя теорему о среднем, будем иметь: 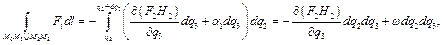
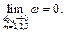 Аналогично, находим:
Аналогично, находим: 
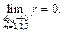
Итак, 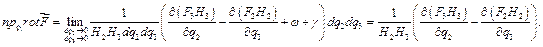
Определив ещё две проекции, получим:
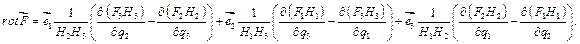
Примеры.
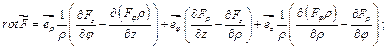
2) сферические координаты:
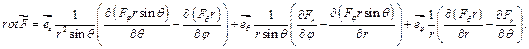
 2015-07-04
2015-07-04 6579
6579