2015-07-04
437
Пусть стационарная накачка поддерживается на уровне, при котором резонансные потери равны нулю (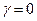
). Все другие потери в резонаторе, естественно, сохраняются. Такой резонатор называется «холодным» или «пассивным».
Рассмотрим изменение поля после полного обхода резонатора:
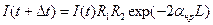. (11.7)
Время полного обхода резонатора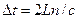 
. Считая, что изменения интенсивности за один обход малы (приближение малых потерь), получим выражение для скорости изменения интенсивности:
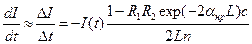. (11.8)
Если ввести обозначение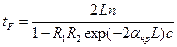 
, то выражение (11.8) можно записать в общем виде, пригодном для описания изменения поля в резонаторе любого типа:
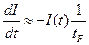. (11.9)
Решение уравнения (11.9) описывает экспоненциальное затухание поля во времени:
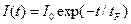. (11.10)
Параметр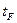 
называется временем жизни фотонов в резонаторе или временем затухания поля в «пассивном» резонаторе. За это время поле в резонаторе, у котором устранены резонансные потери, уменьшается в е раз.
Примеры. Оценка величины .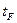
Двухзеркальный резонатор в приближении малых потерь:
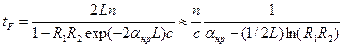(11.11)
Можно записать выражение для 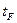в следующем виде:
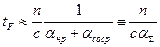, (11.12)
где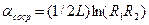 
– условная величина распределенного затухания, эквивалентная сосредоточенным потерям резонатора.
Часто распределенными потерями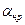 
можно пренебречь по сравнению с сосредоточенными 
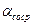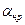>> . В этом случае из (11.2) получим:
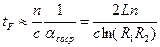. (11.13)
При 1 –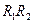 
<< 1 получаем (
, 
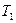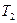– коэффициенты пропускания зеркал по мощности):
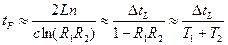. (11.14)
Резонатор импульсного твердотельного лазера:
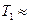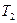0; =0,5;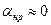 
; 
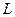=10 см; 
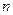= 1,5.
Время обхода резонатора: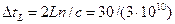 
=1 нс.
Время жизни фотонов: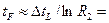 
… нс.
Резонатор непрерывного газового лазера:
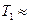0; 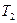=0,01; 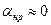; 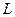=150 см; 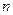= 1.
Время обхода резонатора: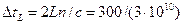 
=10 нс.
Время жизни фотонов: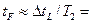 
1 мкс.
Резонатор полупроводникового лазера:
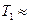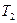0; =0,3; 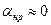; 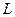= 50 мкм; 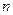= 3.
Время обхода резонатора: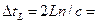 
=1 пс.
Время жизни фотонов: 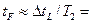3 пс.
