Продолжение

	для r1: (3, 1), (4, 2), (7, 3), (8, 7); для r2: (3, 3), (4, 4), (7, 5), (8, 6)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(A6)³4), d(r1.A1)=a4); r1.A6=r2.A6=A6
	для r1: (3, 1), (4, 2), (7, 3), (8, 6); для r2: (3, 3), (4, 4), (7, 7), (8, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4)p(r1.A1,r2.A4,r2.A5,r1.A6)(r1>q<r2,d(A5)=4); r1.A5=r2.A5=A5
	для r1: (3, 1), (4, 2), (7, 3), (8, 6); для r2: (3, 3), (4, 4), (7, 6), (8, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, r1.A6=r2.A6), d(r1.A1)=a3)
	для r1: (3, 1), (4, 2), (7, 3), (8, 6); для r2: (3, 3), (4, 4), (7, 5), (8, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A2, r1.A3, r2.A4) (r1>q<r2, d(A6)£3); r1.A6=r2.A6=A6
	для r1: (3, 1), (4, 2), (7, 3), (8, 6); для r2: (3, 3), (4, 4), (7, 5), (8, 7)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, (r1.A5=r2.A5)), d(r1.A1)=a3)
	для r1: (3, 1), (4, 2), (7, 3), (8, 6); для r2: (3, 3), (4, 4), (7, 5), (8, 6)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4)p(r1.A1,r2.A4,r2.A5,r2.A6)(r1>q<r2,d(A3)=c6,); r1.A3=r2.A3=A3

Продолжение

	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 4), (2, 5), (5, 6), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A3, r2.A7, r2.A8)(r1>q<r2, d(r1.A8)<d(r2.A8)
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 4), (2, 5), (5, 3), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(A3)=c2); r1.A3=r2.A3=A3
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 4), (2, 2), (5, 3), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A3, r2.A4, r2.A8)(r1>q<r2, d(r1.A7)<d(r2.A8))
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 3), (2, 2), (5, 1), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(A7)<3), d(r1.A3)=c1); r1.A7=r2.A7=A7
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 3), (2, 2), (5, 1), (6, 7)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A3, r1.A4, r2.A8)(r1>q<r2, d(r1.A8)³d(r2.A8))
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 1), (2, 2), (5, 3), (6, 7)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(A3)=c1), d(r1.A4)=d1); r1.A3=r2.A3=A3

Продолжение

	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 1), (2, 2), (5, 7), (6, 6)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A3, A4, A7, r2.A8)(r1>q<r2, d(A4)=d2); r1.A4=r2.A4=A4
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 1), (2, 5), (5, 6), (6, 7)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(r1.A7)<d(r2.A7)), d(r1.A3)=c2)
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 5), (2, 6), (5, 7), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4)p(r1.A1,r1.A2,r2.A5,A6)(r1>q<r2, d(r1.A7)<d(r2.A7))) .
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 3), (2, 4), (5, 7), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, (d(A7)³2)), d(r1.A3)=c1); r1.A7=r2.A7=A7
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 3), (2, 5), (5, 7), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A2, r2.A6) (r1>q<r2, (r1.A7= r2.A7)) .
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 2), (2, 5), (5, 7), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, (r1.A8=r2.A8)), d(r1.A3)=c2)

Продолжение

	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 2), (2, 4), (5, 7), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A2, r1.A5, r2.A6) (r1>q<r2, r1.A7=r2.A7)
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 2), (2, 5), (5, 5), (6, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, (r1.A7=r2.A7)), d(r1.A3)=c1)
	для r1: (1, 1), (2, 2), (5, 7), (6, 8); для r2: (1, 2), (2, 5), (5, 5), (6, 7)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A2, r1.A5, r2.A6) (r1>q<r2, r1.A4=r2.A4)
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 1), (3, 2), (5, 7), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, r1.A6=r2.A6), d(r2.A2)=b1)
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 1), (3, 3), (5, 7), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A2, r1.A3, r2.A5) (r1>q<r2, r1.A6£ r2.A8)
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 1), (3, 3), (5, 4), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, r1.A2=r2.A2), d(r1.A4)=d1)

Продолжение

	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 3), (3, 4), (5, 5), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4)p(r1.A1,r2.A2,r1.A3,r2.A5)(r1>q<r2,d(r1.A6)=d(r2.A6))
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 3), (3, 4), (5, 5), (7, 6)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, r1.A2=r2.A2), d(r2.A6)=1)
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 3), (3, 4), (5, 5), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) p(r1.A1, r2.A4, r2.A5, r1.A6)(r1>q<r2, d(A5)=4); r1.A5=r2.A5=A5
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 2), (3, 4), (5, 5), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4) d((r1>q<r2, d(r1.A6)<d(r2.A8)), d(r1.A2)=b1)
	для r1: (1, 1), (3, 3), (5, 6), (7, 8); для r2: (1, 2), (3, 4), (5, 6), (7, 8)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4)p(r1.A1,r1.A2,r1A6,r2.A5)(r1>q<r2,d(r1.A6)³d(r2.A8))
	для r1: (1, 2), (3, 4), (5, 6), (7, 8); для r2: (1, 1), (3, 2), (5, 4), (7, 6)	1) (r1Èr2); 2) (r1Çr2); 3) (r1\r2); 4).d((r1>q<r2, r1.A6=r2.A6), d(r2.A2)=b1)

4. Логика нечетких множеств и отношений

Часто нужно принимать решение при неполном описании объектов или связей между ними. Например, такие понятия, как "большое входное сопротивление осциллографа", "малое напряжение на базе транзистора", "постоян­ное число оборотов двигателя" дают лишь качественную оценку атрибутов объектов или такие высказывания, как "судно стоит у причала", "самолет находится в аэропорту", "рыбопродукция загружена в дефростер" дают лишь качественное описание связей между объектами, такие суждения, как "если идет дождь, то закрыть все люки", "если продукты вывезены из Африки, то направить их на карантин", "если температура тела 40⁰С, то человек болен" дают качественное описание логики принятия решений.

Задачи качественного описания возникают при проектировании больших систем, распознавании образов, принятии реше­ний в управлении и т.п. Впервые эту проблему поднял Заде в работах [11] и [12].

Неполное описа­ние элемента или ситуации не позволяет оценить меру их принадлежности к определенному классу объектов и с уверенностью дать оценку правильности принимаемого решения.

Для решения подобного класса задач разработана нечеткая логика (fuzzi logic), объектом исследования ко­торой являются нечеткие множества (fuzzi set), нечеткие отношения (fuzzi relation), нечеткие алгебраические операции и нечеткое исчисление (fuzzi calculus).

Наиболее полное описание проблем и методов решения задач нечеткой логики изложены в [5].

4.1 Нечеткие множества

Пусть дано произвольное множество U. Назовем его базовым множеством.

Если на этом множестве задать нечетко некоторое подмноджество X’, то степень принадлежности любого элемента uÎU множеству X’может быть оценена с помощью функции принадлежности:m_x’(u): U ® [0;1].

Функция принадлежности – это некоторое субъективное измерение нечеткой принадлежности элемента заданному множеству и это измерение отличается от вероятностной меры. Под субъективной мерой, как правило, понимается степень принадлежности элемента u_i нечеткому множеству X’, определенная опросом одного или нескольких экспертов. Вероятностная мера, по закону больших чисел, подразумевает знание аналитических зависимостей этой принадлежности.

Значение функции принадлежит замкнутому интервалу [0;1]. Для каждого конкретного элемента uÎU величина m_x(u) принимает конкретное значение на этом интервале. Это значение функции и называют степенью принадлежности элемента uÎU нечеткому множеству X’.

Нечеткое множество X’ записывают так:

X’={m_x’(u₁)/u₁, m_x’(u₂)/u₂,... m_x’(u_n)/u_n}, где u_iÎU, m_x’(u_n)Î[0;1],

где m_x’(u_i) –значение функции принадлежности элемента базового множества u_iÎU нечеткому множеству X’, или степень принадлежности.

Носителем нечеткого множества X’ является “четкое” подмножество X={u₁, u₂,...u_n}ÍU. Носитель нечеткого множества содержит только те элементы U, для которых значение функции принадлежности больше нуля.

Если для некоторого u_iÎU имеем m_x’(u_i)=1, то элемент “четко” принадлежит множеству X’.

Если все элементы носителя X имеют значение m_x’(u_i)=1, то задано “четкое” подмножество множества U, т.е. XÍU.

Если для некоторого u_iÎU имеем m_x’(u_i)=0, то элемент “четко” не принадлежит множеству X’.

Если все элементы носителя X имеют значение m_x’(u_i)=0, то задано “четкое” пустое множество, т. е. X’=Æ.

Пример. Пусть дано 10 шаров. Множество всех подмножеств множества шаров содержит пустое множество, одно-, двух- трех- и т.д. до десятиэлементного подмножества Пусть множество этих подмножеств есть область определения функции принадлежности, т.е. U={Æ, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Необходимо оценить степень принадлежности любого из этих подмножеств нечеткому множеству, заданному понятием “несколько шаров”.

Для подмножеств, содержащих нуль, один, два, половину или все шары, эксперт определил значение функции принадлежности понятию “несколько шаров” равным нулю, так как можно было бы сказать конкретно: “взять половину шаров”, “взять два шара” и т.п.. Для подмножеств, содержащих три, восемь или девять шаров, эксперт определил значение функции принадлежности равным 0, 6, а для подмножеств, содержащих четыре, шесть или семь шаров, - равным 0, 8.

Следовательно, эксперт выполнил поставленную задачу так:

X’={0,6/3; 0,8/4; 0/5; 0,8/6; 0,8/7; 0,6/8; 0,6/9}

Носителем этого нечеткого подмножества X’ является X={3, 4, 6, 7, 8, 9}.

Такова была субъективная мера степени принадлежности каждого подмножества универсального множества нечеткому подмножеству “несколько шаров”.

Пример. Пусть дано множество легковых автомашин, изготавливаемых в России U={“волга”, “жигули”, “москвич”}. Определить их принадлежность классу “хорошая машина”.

Эксперт выполнил эту задачу так:

X’={0,6/”волга”; 0,8/”жигули”; 0,4/”москвич”}.

Это – субъективная оценка эксперта.

Пример. Пусть дан электрический двигатель и эксперт должен отнести значения токов и скорости вращения работающего двигателя в четыре класса: X’₁("нулевой"), X’₂("малый"), X’₃(“средний") и X’₄(“большой"). Пусть величина тока изменяется в пределах от 0 до 21А (базовая шкала), скорость вращения двигателя – от 0 до 3150об/мин.(базовая шкала).

Так как понятия “нулевой”, “малый”, “средний”, “большой” не определены, то для эксперта заданными являются терм-множества:

T₁(“величина тока”)={“нулевая”, “малая”, “средняя”, “большая”};

T₂(“величина скорости вращения”)={“нулевая”, “малая”, “средняя”, “большая”},

где “нулевая”, “малая”, “средняя” и “большая” являются лингвистическими переменными.

Пусть эксперт весь диапазон изменения тока и скорости вращения двигателя разбил на восемь поддиапазонов и установил два уровня степени принадлежности классу “нулевой”, “малый”, “средний”, “большой”: 0,33 и 1,00.

Степень принадлежности, по мнению эксперта, величины тока классу “нулевой”, “малый”, “средний” или “большой” представлены таблицей.

Таблица 4.14

ток (А)	степень принадлежности
“Нулевой”	“Малый”	“Средний”	"Большой”
	0,33	0,33
		0,33	0,33
			0,33	0,33

В этом случае нечеткие множества предметной переменной описаны так:

X’₁₁ ("нулевой" ток) = {I/0; 0,33/3};

X’₁₂ ("малый" ток) = {0,33/3; 1/6; 0,33/9};

X’₁₃ ("средний" ток) = {0,33/9; 1/12; 0,33/15};

X’₁₄ ("большой" ток) = {0,33/15; 1/18; 1/21}.

Степень принадлежности скоростей вращения двигателя классу “нулевая”, “малая”, “средняя” или “большая” представлена табл. 4.15.

Таблица 4.15

скорость (об/мин)	степень принадлежности
“Нулевая”	”Малая”	“Средняя”	“Большая”
	0,33	0,33
		0,33	0,33
			0,33	0,33
		О

В этом случае нечеткие множества предметной переменной описаны так:

X₂₁ ("нулевая" скорость вращения) = {I/0; 0,33/450};

X₂₂ ("малая"скорость вращения = {0,33/450; 1/900; 0,33/1350};

X₂₃ ("средняя" скорость вращения) = {0,33/1350; 1/1800; 0,33/2250};

X₂₄ ("большая"скорость вращения) = {0,33/2250; 1/2700; 1/3150}.

Для того, чтобы согласовывать мнения различных экспертов, удобно построить “гладкий” график функции принадлежности на базовой шкале области определения. Это позволит для каждого конкретного факта или события заданной области определения лучше оценивать принадлежность заданному классу. Построение “гладкой” функции по известному набору значений степени принадлежности в некоторых точках базовой шкалы, или на носителе нечеткого множества, требует использования классических методов аппроксимации. Так метод наименьших квадратов поз­воляет получить достаточно гладкую функцию m (u), которая рав­номерно приближается в смысле среднего квадратического отклонения к заданному набору точек.

m (u)= _{i i =.1}S ^m c_i j_i (u),

где j_i (u) –аппроксимирующие функции, а коэффициенты c_i определяются по условию _{ijj i=.1}S ⁿ _ii=.1S ^m(c_i j_i (u_j)- m (u_j))²®min.

На рис. показана возможная “гладкая” функция, построенная по четырем элементам носителя нечеткого множества.

m (u₃)

m (u₂)

m (u₄)

m (u₁)

u₁ u₂ u₃ u₄

Рис. 4.1 Возможная “гладкая” функции принадлежности.

4.1.1 Определение степени принадлежности

Существует два класса методов определения функции принадлежности m_x(u): прямые и косвенные.

Прямыми методами называют такие, в которых степень принадлежности представленного экземпляра базового множества нечеткому множеству непосредственно задается экспертом или группой экспертов. Прямые методы для одного эксперта отражают его субъективную оценку, а для группы экспертов предполагают некоторую интеграцию мнений экспертов с учетом степени их компетентности. Например, если каждому эксперту придать некоторые весовые коэффициенты a Î[0;1], отражающие степень их компетенции, то интегрированная оценка функции принадлежности может быть определена по формуле m (u)=Sr_i(u) a _i/m, где m- число экспертов, r_i(u)=1, если i-ый эксперт положительно отвечает на вопрос о принадлежности элемента u нечеткому множеству, и r_i(u)=0 в противном случае.

Косвенные методы разбивают общую задачу определения степени принадлежности на ряд более простых подзадач. Одним из таких методов является метод попарного сравнения принадлежности элементов множеству X’.

Пусть дан носитель нечеткого множества X={u₁, u₂, u₃,...u_n} и известны функции принадлежности для каждого элемента нечеткого множества

{m_X’(u₁), m_X’(u₂), m_X’(u₃),...m_X’(u_n)}.

Если составить матрицу смежности М из элементов носителя нечеткого множества X, а позициями представить сравнительные оценки принадлежности нечеткому множеству, т.е. m_X’(u_i)/m_X’(u_j), то уравнение

М_* m_X’(u)=E_*m_X’(u),

где E –собственное значение матрицы M при условии, что Sm_X’(u_i)=1

имеет единственное решение m_X’(u)=(m_X’(u₁); m_X’(u₂); m_X’(u₃);... m_X’(u_n)), соответствующее максимальному собственному значению матрицей смежности М (см. табл. 4.1).

Если матрица сравнительной оценки построена неточно, т. е.

М_* m_X’(u)= λ_max*m_X’(u)≠E_*m_X’(u),

то отклонение λ_max от E можно использовать для оценки точности решения уравнения на данном итерационном шаге

Для улучшения согласования решений полагают на главной диагонали матрицы m_X’(u_i)/m_X’(u_i)=1, а для элементов, симметричных относительно главной диагонали, - m_X’(u_i)/m_X’(u_j)=1/m_X’(u_j)/m_X’(u_i).

Таблица 4.1

M	u1	u2	u3	...	un
u1		mX’(u1)/mX’(u2)	mX’(u1)/mX’(u3)	...	mX’(u1)/mX’(un)
u2	mX’(u2)/mX’(u1)		mX’(u2)/mX’(u3)	...	mX’(u2)/mX’(un)
u3	mX’(u3)/mX’(u1)	mX’(u3)/mX’(u2)		...	mX’(u3)/mX’(un)
...	...	...	...	...	...
un	mX’(un)/mX’(u1)	mX’(un)/mX’(u2)	mX’(un)/mX’(u3)	...

Опрос экспертов о том, насколько элемент u_i более значим, чем элемент u_j проводится по специальной таблице (см. табл. 4.2), где на естественном языке дана интерпретация сравнительной оценки значимости элементов x_i и x_j на базовой шкале [0; 9].

По этим оценкам можно составить матрицу смежности сравнительных оценок М ’(см. табл. 4.3), где r_ij=m_X’(u_i)/m_X’(u_j).

Если вычислить сумму j-го столбца матрицы (см. табл. 4.3), т.е.

Sr_ij =k_j, то при условии Sm_X’(u_i)=1 имеем Sr_ij =S(m_X’(u_i)/m_X’(u_j))= (Sm_X’(u_i))/m_X’(u_j)=1/m_X’(u_j)=k_j.

Или m_X’(u_j)=1/k_j.

Так можно вычислить значения каждой компоненты вектора m_X’(u)=(m_X’(u₁); m_X’(u₂); m_X’(u₃);... m_X’(u_n)).

Таблица 4.2

сравнительные оценки значимости	интерпретация оценок значимости элементов ui /uj
	несравнимая (нет смысла сравнивать)
	одинаковая значимость
	слабая значимость (нет доказательств предпочтения ui /uj)
	существенная значимость (существенные признаки предпочтения ui /uj)
	очевидная значимость (убедительные доказательства предпочтения ui /uj)
	абсолютная значимость (максимальная значимость предпочтения ui /uj)
2, 4, 6, 8	промежуточные оценки
обратные значения	если оценка mX’(ui)/mX’(uj) имеет ненулевое значение, то mX’(uj)/mX’(ui)=1/mX’(ui)/mX’(uj)

Таблица 4.3

M’	u1	u2	u3	...	un
u1		r12	r13	...	r1n
u2	r21		r23	...	r2n
...	...	...	...	...	...
un	rn1	rn2	rn3	...
kj	k1	k2	k3	...	kn

Пример. Пусть для оценки плотности автомобилей на регулируемом перекрестке используется в качестве базового множества числo автомобилей в единицу времени U={0, 5, 10, 15, 20, 25, 30, 35, 40}. Необходимо определить степени принадлежности элементов этого множества нечеткому подмножеству “средняя плотность”. Опросом экспертов по табл. 4.2 получена матрица парных сравнений (см. табл. 4.4), которая после перехода от простых дробей к десятичным представлена табл. 4.5.

Таблица 4.4

M’
		1/2	1/7	1/8	1/9	1/8	1/7	1/2
			1/2	1/5	1/7	1/5	1/2
				1/2	1/5	1/2
					1/2
					1/2
				1/2	1/5	1/2
			1/2	1/5	1/7	1/5	1/2
		1/2	1/7	1/8	1/9	1/8	1/7	1/2

Таблица 4.5

M’
		0,5	0,14	0,125	0,11	0,125	0,14	0,5
			0,5	0,2	0,14	0,2	0,5
				0,5	0,2	0,5
					0,5
					0,5
				0,5	0,2	0,5
			0,5	0,2	0,14	0,2	0,5
		0,5	0,14	0,125	0,11	0,125	0,14	0,5
kj			12,28	5,65	2,9	5,65	12,28

Для определения m_X’(u_j) воспользуемся формулой m_X’(u_j)=1/k_j.

Тогда X’={0,02/0; 0,04/5; 0,08/10; 0,18/15; 0,34/20; 018/25; 0,08/30; 0,04/35; 0,02/40}.

Для проверки точности решения задачи умножим матрицу M’на вектор r=(0,02; 0,04; 0,08; 0,18; 0,34; 018; 0,08; 0,04; 0,02}. В результате получим вектор чисел (0,18; 0,36; 0,85; 1,57; 2,96; 1,57; 0,85; 0,36; 0,18).

Поделим поэлементно значения вектора чисел на значения вектора r. Получим вектор (9; 9; 10,6; 8,7; 8,7; 8,7; 10,6; 9; 9), в котором i-ый элемент есть значение λ_max, соответствующее элементу m_X’(u_i). Среднее значение λ_max равно 9,25. Следовательно, наибольшее отклонение λ_max от E равно 0,25. Следовательно точность решения уравнения равна 0,25/9=0,03. Такая точность достаточна.

Для нормализации нечеткого множества примем, что понятию “средняя плотность” в наибольшей степени соответствует 20 автомобилей в единицу времени. Поэтому степени принадлежности каждого элемента нечеткого множества поделим на степень принадлежности для 20 автомобилей, т.е.

X’={0,06/0; 0,12/5; 0,24/10; 0,53/15; 1/20; 0,53/25; 0,24/30; 0,12/35; 0,06/40}.

Для снижения числа элементов нечеткого множества часто отбрасывают те элементы, степень принадлежности которых достаточно мала. Для этого введем понятие степень разделения - a. и сравним степень принад­лежности каждого элемента множества с заданным значе­нием a. Если для множества “средняя плотность” принять a =0,5, то в нечеткое множество войдут только три группы машин:

X’={0,53/15; 1/20; 0,53/25}.

4.1.2 Операции над нечеткими множествами

Над нечеткими множествами можно исполнить такие же операции, как и над четкими. Отличие заключается в определении степени принадлежности результата этой операции на интервале [0; 1].

Пусть дано базовое множество U = {u₁, u₂, u₃, u₄, u₅, u₆, u₇, u₈, u₉} на основе которого сформированы два нечетких множества:

A’={0,6/ u₁, 0,4/ u₂,0,8/ u₃,0,2/ u₄, 1,0/ u₅, 0,3/ u₆};

B'={0,9/ u₁, 0,4/ u₂, 1,0/ u₃, 0,7/ u₇,0,3/ u₈, 0,5/ u₉}.

Рассмотрим исполнение различных теоретико-множественных операций над этими множест­вами.

Объединение нечетких множествА’ и В’ есть множество С’, состоя­щее из всех тех элементов множества U, которые принадлежат хотя бы одному нечеткому множеству А’ или В’.

C’ = (A’ÈB’).

Степень при­надлежности элемента базового множества нечеткому множеству C’ равна максимальному значению функции принадлежности для нечетких множеств А’ и В’, т.е.

m_С’(u)= m_A(u)Úm_B(u)=max{m_A(u); m_B(u)}.

Для заданных множеств имеем:

С’=(A’ÈB’) ={0,9/u₁, 0,4/u₂, 1,0/u₃, 0,2/u₄, 1,0/u₅, 0,3/u₆, 0,7/u₇, 0,3/u₈, 0,5/u₉}.

Пересечение нечетких множествА’ и В’ есть множество С’, состоящее из всех тех элементов базового множества U, которые принад­лежат и нечеткому множеству А’ и нечеткому множеству В’.

C’ = (A’ÇB’).

Степень при­надлежности элемента базового множества нечеткому множеству C’ равна минимальному значению функции принадлежности для нечетких множеств А’ и В’, т.е.

m_С’(u)=m_A’(u)&m_B’(u)=min(m_A’(u); m_B’(u)}.

Для заданных множеств имеем:

С’=(АÇВ)={0,6/u₁,0,4/u₂, 0,8/ u₃}.

Дополнение нечеткого множестваA’ есть нечеткое множество ùA’, состоящее из всех элементов универсального множества U, которые не принадлежат нечет­кому множеству А’.

Степень при­надлежности элемента нечеткому множеству ùA’ равна дополнению до значения степени принадлежности базовому множеству U, т.е.

m_ùA’(u)= 1 - m_A’(u).

Для заданных множеств имеем:

ùВ’={0,1/u₁, 0,6/u₂, 1,0/u₄, 1,0/u₅, 1,0/u₆, 0,3/u₇, 0,7/u₈, 0,5/u₉};

ùА’={0,4/u₁, 0,6/u₂, 0,2/u₃, 0,8/u₄, 0,7/u₆, 1,0/u₇, 1,0/u₈, 1,0/u₉}.

Разность нечетких множествА’ и В’ есть множество С’, состоящее из тех элементов универсального множества U, которые при­надлежат нечеткому множеству А’ и не принадлежат нечеткому множест­ву В’.

C’=A’\B’=A’ÇùB’.

Степень при­надлежности элемента базового множества нечеткому множеству C’ равна минимальному значению функции принадлежности для нечетких множеств А’ и ùВ’, т.е.

m_С’(u)=m_A’(u)&(1-m_B’(u))=min{m_A’(u); (1-m_B’(u))}.

Для заданных множеств имеем:

С’=А’\В’={0,1/u₁, 0,4/u₂, 0,2/u₄, 1,0/u₅, 0,3/u₆}.

Симметрическая разность нечетких множествА’ и В’ есть множество С’, состоящее из всех тех элементов универсального множества U, которые принадлежат нечеткое множеству А’ и не принадлежат нечеткому множеству В’ или принадлежат нечеткому множеству В’ и не при­надлежат нечеткому множеству А’.

С’=А’ÑВ’=(А’ÇùВ’)È(В’ÇùА’).

Степень при­надлежности элемента базового множества нечеткому множеству C’ равна максимальному значению двух минимальных значений для множеств (А’ÇùВ’) и (В’ÇùА’), т.е.

m_C’(u)=(m_A’(u)&m_ùB’(u))Ú (m_B’(u)m_ùA’(u_i))=

max{min{m_A’(u);m_ùB’(u)};min{m_B’(u);m_ùA’(u_i)}}.

Для заданных множеств имеем:

С’=А’ÑВ’= {10,4/u₁, 0,4/u₂, 0,2/u₃, 0,2/u₄, 1,0/u₅, 0,3/u₆, 0,3/u₇, 0,3/u₈, 0,5/u₉}.

Прямое произведение нечетких множествА’ и В’ есть множество C’, состоящее из всех тех или только тех упо­рядоченных пар

(u_i; u_j), первая компонента которых принадлежит множеству А’, а вторая - множеству В’.

C’=А’ÄВ’.

Степень при­надлежности упорядоченной пары (u_i; u_j) нечеткому множеству C’ равна минимальному значению функций принадлежности элементов u_iÎA’ и u_jÎB’, т.е

m_С’ (u_i,u_j) = m_A’ (u_i)&m_B’ (u_j) = min {m_A’ (u_i); m_B’ (u_j)}.

Для заданных множеств имеем матрицу смежности элементов нечетких множеств (см. табл. 4.6).

Таблица 4.6

C’	uj =u1	uj =u2	uj =u3	uj =u7	uj =u8	uj =u9
u1=ui	0,6	0,4	0,6	0,6	0,3	0,5
u2=ui	0,4	0,4	0,4	0,4	0,3	0,4
u3=ui	0,8	0,4	0,8	0,7	0,3	0,5
u4=ui =ui	0,2	0,2	0,2	0,2	0,2	0,2
u5=ui	0,9	0,4	1,0	0,7	0,3	0,5
u6=ui	0,3	0,3	0,3	0,3	0,3	0,3

На нечетких множествах могут быть рассмотрены также операции включения одного множества в другое и их сравнения.

Включение нечеткого множестваA’ в множество B’.

Степень включения n(A’, B’) нечеткого множества A’ в нечеткое множество B’ определяется по формуле:

n(A’, B’)= &(m_A’ (u)®m_B’ (u))= &(m_ùA’ (u)Ú m_B’ (u))=min{max{(1-m_A’(u)); m_B’(u)}}.

При этом операции дополнения, дизъюнкции и конъюнкции выполняются для каждого элемента базового множества.

Если n (A’, B’)³0,5, то множество A’ нечетко включено в множество B’.

Пример. Пусть U={u₁, u₂, u₃, u₄, u₅},

A’={0,3/u₂; 0,6/u₃; 0,4/u₅}, B’={0,8/u₁; 0,5/u₂; 0,7/u₃; 0,6/u₅}.

Тогда n(A’, B’)=min{max{1/u₁; 0,8/u₁}; max{0,7/u₂; 0,5/u₂}; max{0,4/u₃; 0,7/u₃}; max{1/u₄;0/u₄}; max{0,6/u₅; 0,6/u₅}}=min{1/u₁; 0,7/u₂; 0,7/u₃; 1/u₄; 0,6/u₅}=0,6. Таким образом нечеткое множество A’ нечетко включено в нечеткое множествоB’.

Равенство нечетких множествA’ и B’.

Степень равенства нечетких множеств A’ и B’ определяется по формуле:

n(A’,B’)=&(m_A’(u)«m_B’(u))=&((m_ùA’(u)Úm_B’(u))&(m_ùB’(u)Úm_A’(u)))=

min{min{max{(1-m_A’(u)); m_B’(u)}; max{(1-m_B’(u)); m_A’(u)}}}.

При этом операции дополнения, дизъюнкции и конъюнкции выполняются для каждого элемента базового множества.

Если n (A’, B’)³0,5, то множества A’ и B’ нечетко равны.

Пример. Пусть U={u₁, u₂, u₃, u₄, u₅},

A’={0,8/u₂; 0,6/u₃; 0,1/u₅}, B’={0,3/u₁; 0,6/u₂; 0,7/u₃; 0,2/u₄; 0,3/u₅}.

Тогда n(A’, B’)=min{min{max{1/u₁; 0,3/u₁}; max{0/u₁; 0,7/u₁}}; min{max{0,2/u₂; 0,6/u₂}; max{0,8/u₂; 0,4/u₂}}; min{max{0,4/u₃; 0,7/u₃}; max{0,6/u₃; 0,3/u₃}}; min{max{1/u₄;0,2/u₄}; max{0/u₄;0,8/u₄}}; min{max{0,9/u₅; 0,3/u₅}; max{0,1/u₅; 0,7/u₅}}=min{min{1/u₁; 0,7/u₁}; min{0,6/u₂; 0,8/u₂}; min{ 0,7/u₃; 0,6/u₃}; min{1/u₄; 0,8/u₄}; min{0,9/u₅; o,7/u₅}}=min{0,7/u₁; 0,6/u₂; 0,6/u₃; 0,8/u₄;0,7/u₅}=0,6. Таким образом нечеткие множества A’ и B’ нечетко равны.

4.2 Нечеткие соответствия и отношения

Наряду с нечеткими множествами можно описать нечеткие соответствия и отношения, которые являются подмножест­вами прямого произведения двух множеств, т.е. {(x, y)}ÍXÄY или {(x_i, x_j)}ÍXÄX. Следует напомнить, что соответствие есть неоднозначное отображение множества X на множество Y, когда каждому прообразу (xÎX) может соответствовать один или несколько образов (yÎY), а каждому образу (yÎY) может соответствовать один или несколько прообразов (xÎX), а отношение – есть неоднозначное отображение между элементами одного множества X.

Отображение удобно представить в операторной форме q: X®Y или

r: X®X, когда между элементами двух множеств устанавливается логическая связка импликации.

При этом принадлежность элементов множествам X и Y может быть задана четко, но нечетко определено отображение. Функция принадлежности m_q’(x_i,y_j)/(x_i,y_j) или m_r’(x_i,x_j)/(x_i,x_j) позхволяет определить степень принадлежности пары элементов (x_i,y_j) или (x_i,x_j) нечетким соответствию или отношению, т.е.

q’={m_r’(x_i,y_j)/(x_i,y_j)};

r’={m_r’1(x_i,x_j)/(x_i,x_j)}.

Нечеткие соответствия и отношения могут быть заданы перечислением всех пар элементов с указанием значения степени принадлежности нечеткому соответствию или отношению или с помощью матриц. Строки и столбцы матриц заданы элементами xÎX и yÎY или только xÎX, а позиции - значениями m_q’(x_i,y_j) или m_r’(x_i,x_j). В первом случае (для m_q’(x_i,y_j)) задана матрица инциденции, во втором (для m_r’1(x_i,x_j))– матрица смежности.

Если дано n-арное соответствие q’(x₁, x₂, ¼,x_n, y): Xⁿ®Y или отношение r’(x₁, x₂, ¼,x_n):X^n-1®X, то значение функции принадлежности должно быть найдено для каждого набора (x_1i, x_2i, ¼,x_ni, y_i) или (x_1i, x_2i, ¼,x_ni), т.е.

m_q’ (x₁, x₂, ¼,x_n, y_i) или m_r’ (x₁, x₂, ¼,x_n).

Пример. Даны множество руководителей магазинов розничной торговли

Х = { x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂ } и множество руководителей фирм Z = { z₁, z₂, z₃, z₄ }.

Для выбора местоположения магазинов относительно местоположения фирм большое значение имеют признаки, на которые обращают внимание руководители магазинов при выборе и приобретении товаров и руководители фирм при заключении договоров. Пусть с помощью экспертов установле­но, что такими признаками являются: y₁ – доступность мага­зина для фирмы; y₂ - высокое качество товара, y₃ - высокий уровень обслуживания, y₄ - низкие цены на товар, т.е. Y={y₁, y₂, y₃, y₄}.

Эксперты, обсуждая с руководителями магазинов и фирм значимость признаков в организации торговли, установили нечеткое их понимание значимости того или иного признака.

Нечеткое понимание может быть описано нечетким соответствием мнения руководителей магазинов и признаков в виде:

q’₁={m_q’(x₁,y₁)/(x₁,y₁), m_q’(x₂,y₁)/(x₂,y₁),... m_q’(x₁₂,y₄)/(x₁₂,y₄)}

и представлено матрицей инциденции (например, табл. 4.7), а нечеткое соответствие руководителей фирм и признаков в виде:

q’₂={m_q’ (y₁,z₁)/(y₁,z₁), m_q’ (y₂,z₁)/(y₂,z₁),...m_q’(y₄,z₄)/(y₄,z₄)}

и представлено также матрицей инциденции (например, табл. 4.8).

В табл. 4.7 элементы каждой строки выражают нечеткую степень значимости (или принадлежности) того или иного признака для конкретного руководителя магазина­. Например, для x₁ – значима только доступность магазина (y₁), или степень принадлежности равна “1”, для x₂ – только качество товара (y₂), для x₃ – только уровень обслуживания (y₃), для x₄ – только низкие цены (y₄), а для x₈ - наибольшее значение имеют качество товара (y₂) и уровень обслуживания (y₃), или степень принадлежности каждого из признаков равна “0,8”, для x₅ - важны все признаки, или степень принадлежности равна “1”, для x₉ – все они безразличны, или степень принадлежности равна “0,5”, а для x₁₁ - все они незначимы, или степень принадлежности равна “0,1”.

q’2	z1	z2	z3	z4
y1	0,9	0,1	0,5	0,7
y2	0,5	0,9	0,6	0,6
y3	0,4	0,9	0,5	0,4
y4	0,8	0,1	0,5	0,6

таблица 4.7 таблица 4.8

q’1	y1	y2	y3	y4
x1
x2
x3
x4
x5
x6	0,8	0,4	0,5	0,9
x7	0,7	0,3	0,4	0,8
x8	0,5	0,8	0,8	0,2
x9	0,5	0,5	0,5	0,5
x10	0,6	0,7	0,8	0,5
x11	0,1	0,1	0,1	0,1
x12

В табл. 4.8 элементы каждой строки выражают нечеткую степень принадлежности признака для руководителя фирмы. Например, для z₁ наиболее значимы доступность магазина (y₁) и низкие цены (y₄), для z₂ –высокие качество товара (y₂) и уровень обслуживания (y₃), для z₃ – все они безразличны, для z₄ – незначим только уровень обслуживания (y₃).

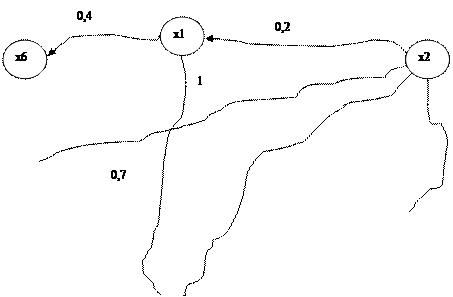
Пример. Пусть в результате стихийного бедствия нарушилось транспортное сообщение между населенными пунктами x₁, x₂, x₃, x₄, x₅, x₆. Эксперты определили нечетко возможную связь между населенными пунктами (степень принадлежности нечеткому множеству) так, как представлено на рис.4.2. В соответствии с графом составлена нечеткая матрица смежности (см. табл. 4.9).

0,1

0,6

		0,8

	0,5

Рис.4.2 Граф смежности населенных пунктов

Таблица 4.9

r’	x1	x2	x3	x4	x5	x6
x1						0,4
x2	0,2		0,8	0,6	0,1
x3		0,8			0,7
x4		0,6			0,5
x5		0,1	0,7	0,5
x6

Эта таблица показывает степень принадлежности двухсторонней связи между населенными пунктами (x₁,x₄), (x₂,x₃), (x₂,x₄), (x₂,x₅), (x₃,x₅),(x₄,x₅), и односторонней связи между населенными пунктами (x₁,x₆), (x₂, x₁). На главной диагонали m (x_i,x_i)=1, так как каждый пункт достижим для самого себя.

4.2.1 Операции над нечеткими соответствиями и отношениями

Поскольку нечеткие соответствия и отношения есть множества, т.е. q’={m_r’(x_i,y_j)/(x_i,y_j)}и r’={m_r’ (x_i,x_j)/(x_i,x_j)}, то к ним применимы все теоретико-множественные операции.

Объединение нечетких соответствийq’₁={m_q’1(x_i,y_j)/(x_i,y_j)} и q’₂={m_q’2(x_i,y_j)/(x_i,y_j)} есть нечеткое соответствие q’=(q’₁Èq’₂), степень принадлежности которому каждой пары (x_i,y_j) определяется формулой

m_q’(x_i,y_j)= m_q’1(x_i,y_j)Úm_q’2(x_i,y_j) =max{m_q’1(x_i,y_j); m_q’2(x_i,y_j)}.

Пример.

q1

y2

y3

y4

q2