Медиана

Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.

Сначала определяют номер медианы:

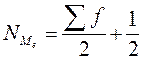Медиана в дискретных и интервальных рядах определяется по разному.

Медиана в дискретном вариационном ряду находится непосредственно по определению на основе накопленных частот.

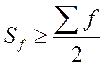Медиана находится там, где накопленная частота равна или превышает полусумму частот:

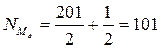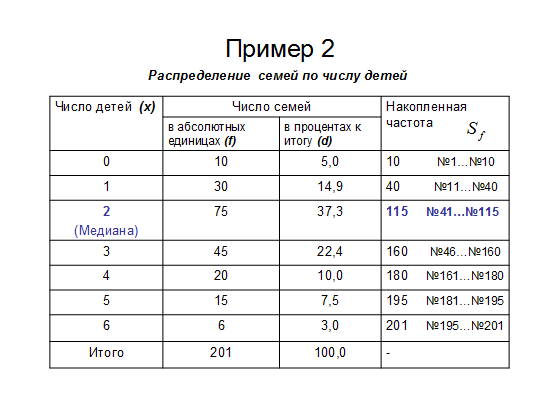
В примере 2

Из таблицы видно, что 101 семья находится там, где накопленная частота 115 (№41…№115)

В интервальных вариационных рядах сначала также находят номер медианы, а затем медианный интервал на основе накопленных частот.

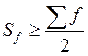Медианный интервал находится там, где накопленная частота равна или превышает полусумму частот:

В медианном интервале для определения значения медианы используют формулу:

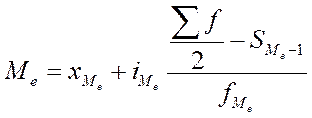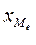где - минимальная граница медианного интервала;

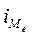- величина медианного интервала;

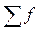- сумма частот;

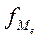- частота медианного интервала;

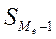
- накопленная частота интервала, предшествующего медианному.

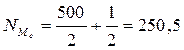
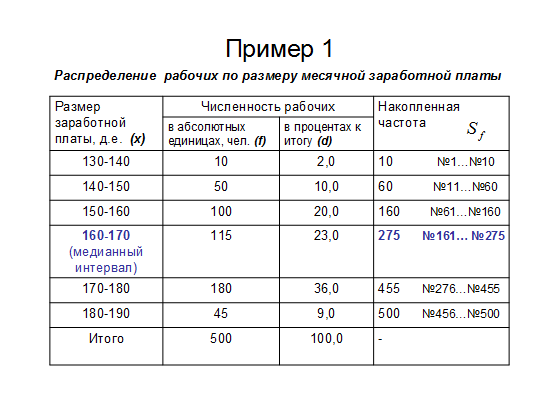
В примере 1 номер медианы

медианный интервал 160-170, а медиана будет равна

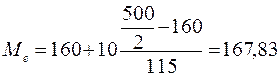160 - минимальная граница медианного интервала;

10 - величина медианного интервала;

500 - сумма частот;

160 - накопленная частота интервала, предшествующего медианному;

115 - частота медианного интервала.

Медиану можно определить и графическим способом, из кумуляты распределения.